复合材料力学涉猎——单层的刚度和强度

1 绪论
- 1.1 复合材料
- 1.2 单层及模型假设
2 单层的正轴刚度
- 2.1 单层的正轴应力-应变关系
- 2.2 单层正轴刚度系数的取值范围
3 单层的偏轴刚度
4 单层的三维应力-应变关系
5 单层板的强度
6 总结

1 绪论

1.1 复合材料

复合材料是一种多相固体材料，是指由两种或者两种以上具有不同的化学或物理性质的组分材料组成的一种与组分材料性质不同的新材料，且各组分之间具有明显的截面。

相对于金属材料，复合材料有自己的特点，比如比强度高、比模量高等。
在低应力的交变载荷作用下，复合材料构件从纤维或基体的薄弱环节开始形成裂纹，逐渐扩展到基体与纤维的结合面上，结合面具有阻止裂纹扩展或改变扩展方向的作用。
碳纤维-铝合金复合材料在400℃高温下，强度和弹性模量基本无变化。有的复合材料具有良好的烧蚀性能。
正是由于符合材料具有性能上的一系列特点，目前飞行器结构设计越来越多地使用复合材料。复合材料结构设计具有两个重要特性：可设计性、可成型性。

1.2 单层及模型假设

纤维增强符合材料是由两种基本原材料——基体和纤维组成的，构成复合材料的基本单元是单层板（简称单层、又名铺层）。纤维可以是连续的、非连续的、编制的、单向的、双向的或者随机分布的。

以力学角度分析复合材料，一般可分为宏观力学方法和细观力学方法。
前者以复合材料的单层、层合板或层合板结构作为研究对象，分析复合材料变现的力学性能，忽略两相材料各自性能差别及相互作用，将两相材料反映在平均的表现性能上。
后者考虑两相材料的各自性能及其相互作用，研究其如何反映在平均的表现性能上（宏观的力学性能上）。

用宏观力学分析方法分析是，假设单层为连续、均匀、正交各向异性的材料；而用细观力学方法时，除宏观假设与上述相同外，还需要细观假设各组分材料是均匀（细观单层是均匀的）、连续、各向同性的材料，并将这些分析限于线弹性与小变形的范围内。

本文将讨论单向纤维增强单层的刚度和强度，给出宏观力学分析方法的结果。

涉及的知识：材料力学、弹性力学、高等数学、线性代数。

2 单层的正轴刚度

单层的正轴刚度是指单层在正轴方向（即单层材料的弹性主方向，如图中 $x_{1}$ ， $x_{2}$ 方向。例如碳纤维-环氧复合材料单层中的碳纤维铺层方向）所显示的刚度性能。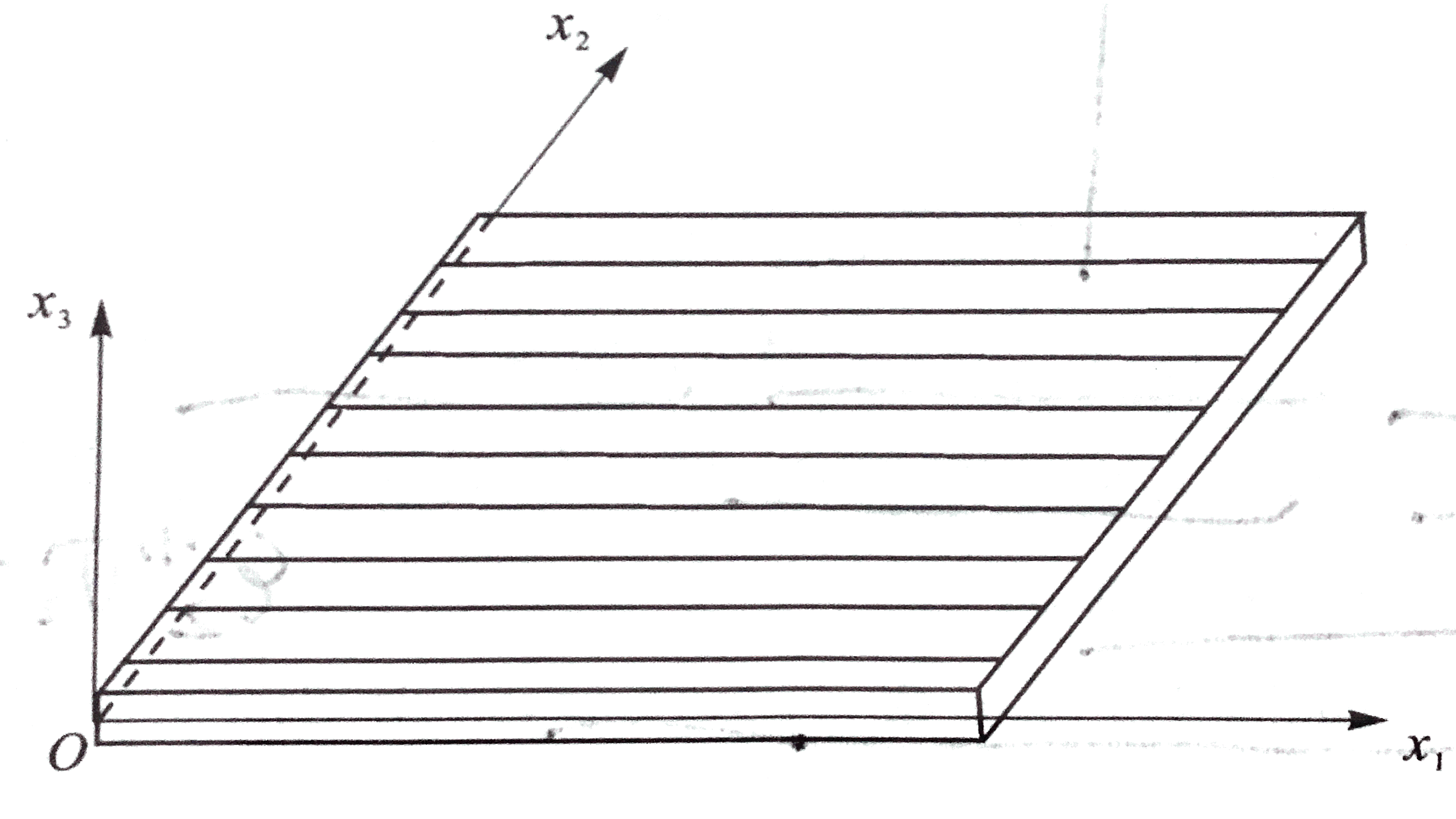
在任意坐标系Oxyz下的单层
假设讨论的复合材料限于在线弹性和小变形的情况下，材料力学中的应变叠加原理仍能适用于复合材料。

2.1 单层的正轴应力-应变关系

如图所示，单层在正轴下的平面应力状态只有三个应力分量 $σ_{1}$ 、 $σ_{2}$ 、 $τ_{12}$ 。书中约定应力的符号规则为：正面正向或负面负向均为正，否则为负。（注意书中下标位置和弹性力学中相比是交换了的，即 $τ_{12}$ 在书中表示在以2为法线的平面上沿1方向的剪应力；而在弹性力学中是指在以1为法线的平面上沿2方向的剪应力。由于 $τ_{12} = τ_{21}$ ，这个区别在大多数情况下无需区分。）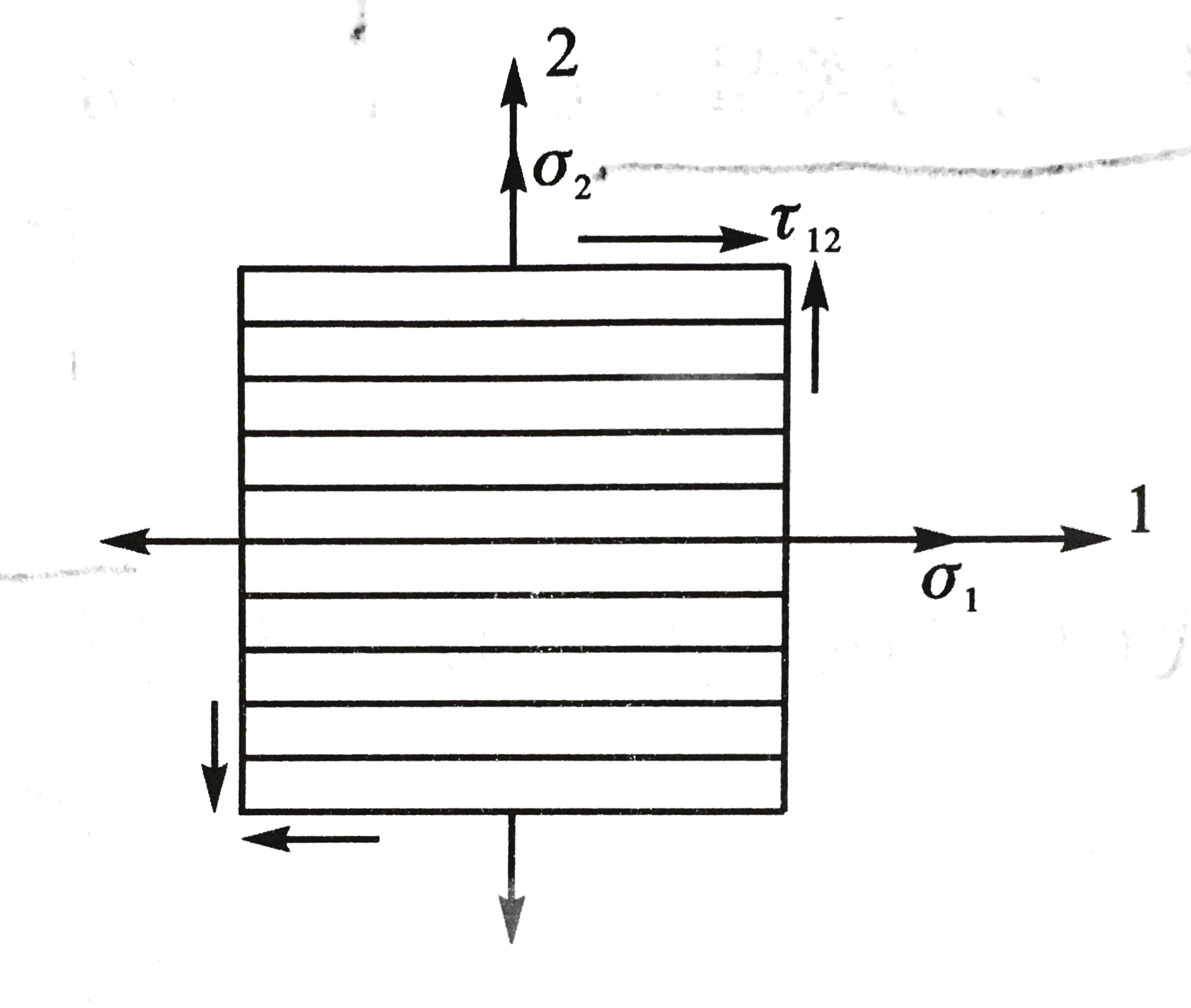
在任意坐标系Oxyz下的单层
书中约定线应变伸长为正，缩短为负；剪应变与两个坐标方向一致的直角变小为正，变大为负。（与弹性力学一致）

因此，由 $σ_{1}$ 引起的应变为：

ϵ_{1}^{(1)} = \frac{1}{E _{L}} σ_{1} ϵ_{2}^{(1)} = - \frac{ν _{L}}{E _{L}} σ_{1}}

由 $σ_{2}$ 引起的应变为：

ϵ_{1}^{(2)} = - \frac{ν _{T}}{E _{T}} σ_{2} ϵ_{2}^{(2)} = \frac{1}{E _{T}} σ_{2}}

由 $τ_{12}$ 引起的应变为

γ_{12} = \frac{1}{G _{L T}} τ_{12}

利用应变叠加原理可得单层在正轴方向的应变-应力关系式为：

ϵ_{1} = \frac{1}{E _{L}} σ_{1} - \frac{ν _{T}}{E _{T}} σ_{2} ϵ_{2} = - \frac{ν _{L}}{E _{L}} σ_{1} + \frac{1}{E _{T}} σ_{2} γ_{12} = \frac{1}{G _{L T}} τ_{12} ⎭ ⎪ ⎬ ⎪ ⎫ (2.1.1)

式中， $E_{L}$ 为纵向弹性模量； $E_{T}$ 为横向弹性模量； $ν_{L}$ 为纵向泊松比； $ν_{T}$ 为横向泊松比； $G_{L T}$ 为面内剪切弹性模量。
这些量称为弹性的正轴工程弹性常数，一共5个，采用功的互等原理，可以证明

\frac{ν _{L}}{ν _{T}} = \frac{E _{L}}{E _{T}} (2.1.2)

因此，单层板独立的工程弹性常数为4个。

将应变-应力关系式 $(2.1.1)$ 写成矩阵的形式：

⎣ ⎢ ⎡ ϵ_{1} ϵ_{2} γ_{12} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ \frac{1}{E _{L}} - \frac{ν _{L}}{E _{L}} 0 - \frac{ν _{T}}{E _{T}} \frac{1}{E _{T}} 0 00 \frac{1}{G _{L T}} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{1} σ_{2} τ_{12} ⎦ ⎥ ⎤

令：

S_{11} = 1 / E_{L} S_{22} = 1 / E_{T} S_{66} = 1 / G_{L T} S_{12} = - ν_{T} / E_{T} S_{21} = - ν_{L} / E_{L}

这些量被称为柔性分量。用柔性分量表示的单层板正轴应变-应力关系式为：

⎣ ⎢ ⎡ ϵ_{1} ϵ_{2} γ_{12} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ S_{11} S_{21} 0 S_{12} S_{22} 0 00 S_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{1} σ_{2} τ_{12} ⎦ ⎥ ⎤ (2.1.3)

由上式可以解得应变表示的应力，得到单层板正轴应力-应变关系式：

⎣ ⎢ ⎡ σ_{1} σ_{2} τ_{12} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ Q_{11} Q_{21} 0 Q_{12} Q_{22} 0 00 Q_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{1} ϵ_{2} γ_{12} ⎦ ⎥ ⎤ (2.1.4)

其中模量分量为：

Q_{11} = m E_{L} Q_{22} = m E_{T} Q_{66} = G_{L T} Q_{12} = m ν_{T} E_{T} Q_{21} = m ν_{L} E_{L} m = (1 - ν_{L} ν_{T})^{- 1}

模量矩阵和柔量矩阵是互逆的。且 $Q_{12} = Q_{21}$ ， $S_{12} = S_{21}$ 。可以看出无论是模量还是柔量其独立分量都为4个。

2.2 单层正轴刚度系数的取值范围

由能量守恒原理可以证明，单层的弹性模量、具有重复下表的柔量分量及模量分量均为正值：

E_{L}, E_{T}, G_{L T} > 0 (2.1.5)

S_{11}, S_{22}, S_{66} > 0

Q_{11}, Q_{22}, Q_{66} > 0

同时可以证明，有：

1 - ν_{L} ν_{T} > 0

ν_{L}^{2} < E_{L} / E_{T} ν_{T}^{2} < E_{T} / E_{L}} (2.1.6)

式 $(2.1.2)$ 、 $(2.1.5)$ 和 $(2.1.6)$ 被称为单层作为正交各向异性材料的工程弹性常数的限制条件。

这些工程弹性常数通常是由实验测得。

3 单层的偏轴刚度

偏轴是指选用的直角坐标系 $O x y z$ 和单层的正轴坐标系 $O x_{1} x_{2} x_{3}$ 的关系为： $x_{3}$ 轴与 $z$ 轴方向相同， $x_{1}$ 、 $x_{2}$ 轴相对于 $x$ 、 $y$ 轴的夹角为 $θ$ （铺层角，逆时针为正）。
设

m = c o s θ, n = s i n θ

3.1 应力转换与应变转换关系

两个不同直角坐标系之间的应力转换是静力平衡条件，应变转换是几何问题，均与材料的物理性质无关，材料力学和弹性力学中对各向同性材料所推导的转换公式完全适用于各项异性材料。

如图所示，分别用垂直 $x_{1}$ 轴和 $x_{2}$ 轴的斜截面在单元体上截出分离体，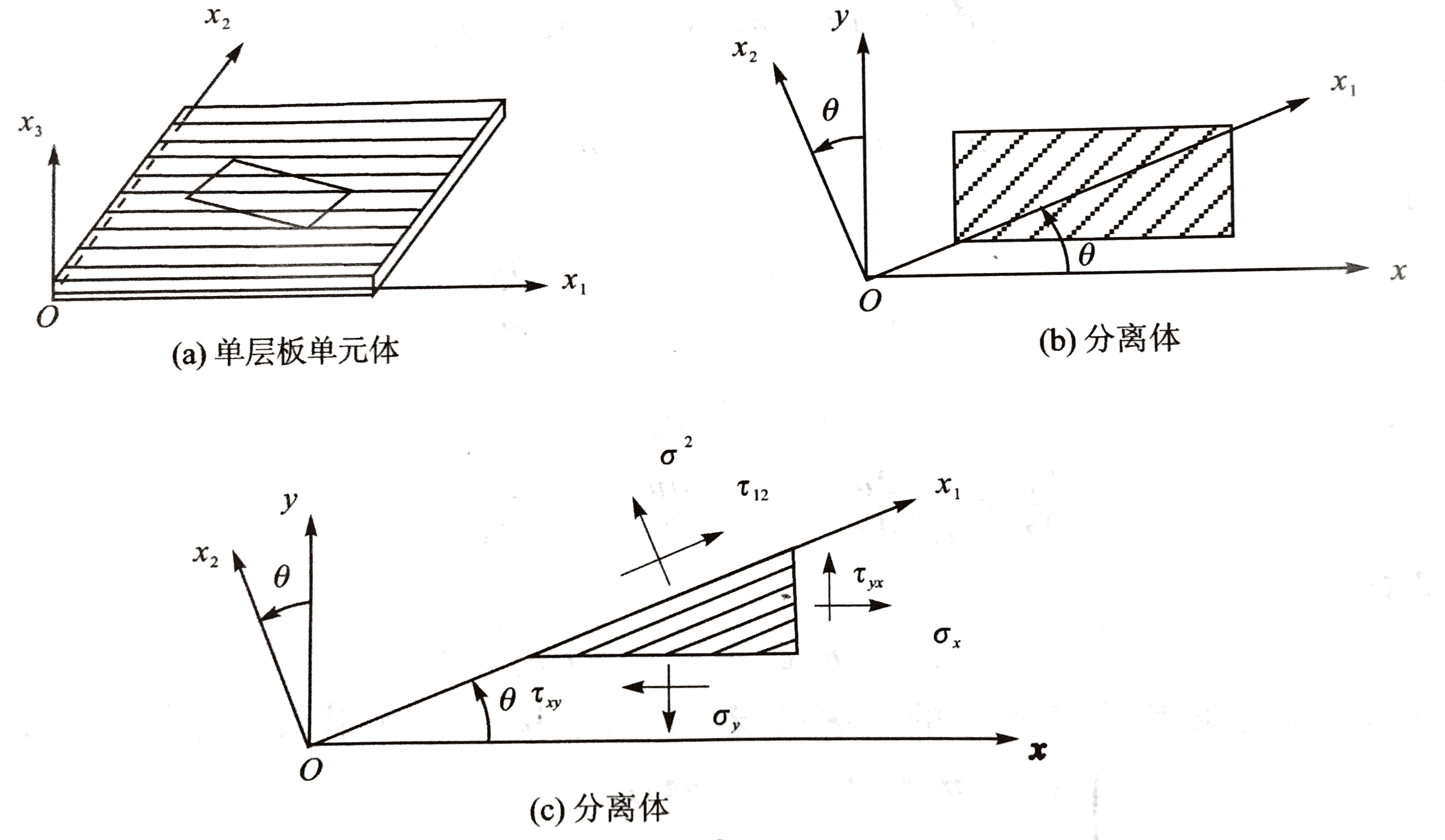
在正轴坐标系123下的单层
根据静力平衡条件可得：

σ_{1} = σ_{x} m^{2} + σ_{y} n^{2} + 2 τ_{x y} m n σ_{2} = σ_{x} n^{2} + σ_{y} m^{2} + 2 τ_{x y} m n τ_{12} = (σ_{y} - σ_{x}) m n + τ_{x y} (m^{2} - n^{2}) ⎭ ⎪ ⎬ ⎪ ⎫ (3.1.1)

写成矩阵的形式：

⎣ ⎢ ⎡ σ_{1} σ_{2} τ_{12} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ m^{2} n^{2} - m n n^{2} m^{2} m n 2 m n - 2 m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ 或 ⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ m^{2} n^{2} m n n^{2} m^{2} - m n - 2 m n 2 m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{1} σ_{2} τ_{12} ⎦ ⎥ ⎤ (3.1.2)

如图所示，平面内一点 $O$ 在外力作用下移动到 $O^{'}$ 点，它在 $O x y$ 坐标系和 $O x^{'} y^{'}$ 坐标系中的位移分别用 $u$ 、 $v$ 和 $u^{'}$ 、 $v^{'}$ 表示，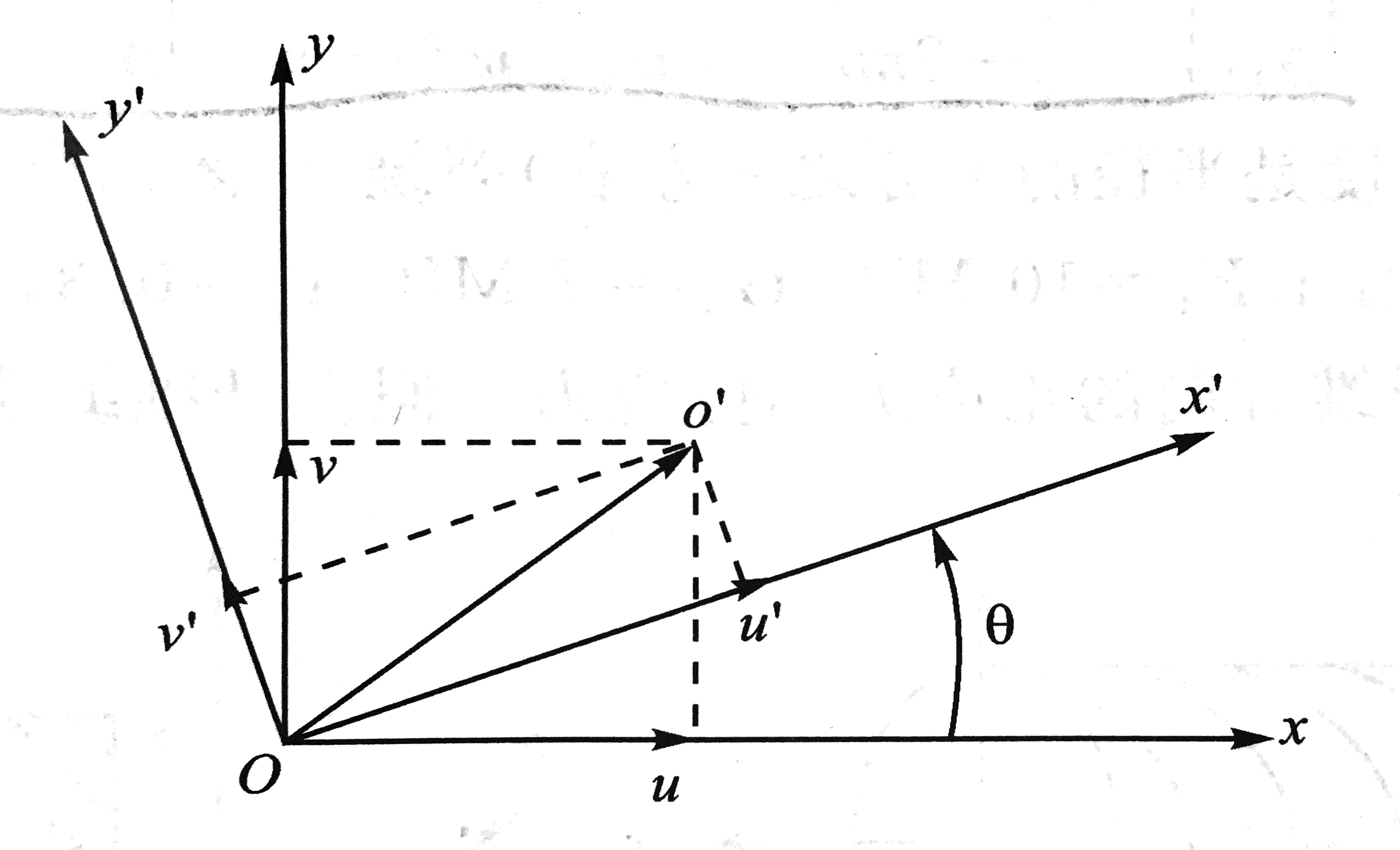
在正轴坐标系123下的单层
则存在下列关系：

u^{'} = m u + n v, v^{'} = - n u + m v x = m x^{'} - n y^{'}, y = n x^{'} + m y^{'}

由链式求导法则：

\frac{\partial u ^{'}}{\partial x ^{'}} = m^{2} \frac{\partial u}{\partial x} + n^{2} \frac{\partial v}{\partial y} + m n (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}) \frac{\partial v ^{'}}{\partial y ^{'}} = n^{2} \frac{\partial u}{\partial x} + m^{2} \frac{\partial v}{\partial y} - m n (\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}) \frac{\partial u ^{'}}{\partial y ^{'}} = - m n (\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) + m^{2} \frac{\partial u}{\partial y} - n^{2} \frac{\partial v}{\partial x} \frac{\partial v ^{'}}{\partial x ^{'}} = - m n (\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) + m^{2} \frac{\partial v}{\partial x} - n^{2} \frac{\partial u}{\partial y}

结合弹性力学几何方程：

ϵ_{x} = \frac{\partial u}{\partial x}, ϵ_{y} = \frac{\partial v}{\partial y}, γ_{x y} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} ϵ_{x^{'}} = \frac{\partial u ^{'}}{\partial x ^{'}}, ϵ_{y^{'}} = \frac{\partial v ^{'}}{\partial y ^{'}}, γ_{x^{'} y^{'}} = \frac{\partial u ^{'}}{\partial y ^{'}} + \frac{\partial v ^{'}}{\partial x ^{'}}

得：

ϵ_{x^{'}} = m^{2} ϵ_{x} + n^{2} ϵ_{y} + m n γ_{x y} ϵ_{y^{'}} = m^{2} ϵ_{x} + n^{2} ϵ_{y} + m n γ_{x y} γ_{x^{'} y^{'}} = - 2 m n (ϵ_{x} + ϵ_{y}) + (m^{2} - n^{2}) γ_{x y} ⎭ ⎪ ⎬ ⎪ ⎫

将下标 $x^{'}$ 、 $y^{'}$ 换成 $1$ 、 $2$ 得：

ϵ_{1} = m^{2} ϵ_{x} + n^{2} ϵ_{y} + m n γ_{x y} ϵ_{2} = m^{2} ϵ_{x} + n^{2} ϵ_{y} + m n γ_{x y} γ_{12} = - 2 m n (ϵ_{x} + ϵ_{y}) + (m^{2} - n^{2}) γ_{x y} ⎭ ⎪ ⎬ ⎪ ⎫ (3.1.3)

写成矩阵的形式：

⎣ ⎢ ⎡ ϵ_{1} ϵ_{2} γ_{12} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ m^{2} n^{2} - 2 m n n^{2} m^{2} 2 m n m n - m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤ 或 ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ m^{2} n^{2} 2 m n n^{2} m^{2} - 2 m n - m n m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{1} ϵ_{2} γ_{12} ⎦ ⎥ ⎤ (3.1.4)

3.2 单层的偏轴应力-应变关系

将 $(3.1.2)$ 和 $(3.1.4)$ 代入 $(2.1.4)$ 得：

⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ m^{2} n^{2} m n n^{2} m^{2} - m n - 2 m n 2 m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ Q_{11} Q_{21} 0 Q_{12} Q_{22} 0 00 Q_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ m^{2} n^{2} - 2 m n n^{2} m^{2} 2 m n m n - m n m^{2} - n^{2} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤

可简写成

⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ \overline{Q}_{11} \overline{Q}_{21} \overline{Q}_{61} \overline{Q}_{12} \overline{Q}_{22} \overline{Q}_{62} \overline{Q}_{16} \overline{Q}_{26} \overline{Q}_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤ (3.2.1)

其中 $\overline{Q}_{i j} (i, j = 1, 2, 6)$ 被称为偏轴模量分量：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{Q}_{11} \overline{Q}_{22} \overline{Q}_{12} \overline{Q}_{66} \overline{Q}_{16} \overline{Q}_{26} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ m^{4} n^{4} m^{2} n^{2} m^{2} n^{2} m^{3} n m n^{3} n^{4} m^{4} m^{2} n^{2} m^{2} n^{2} - m n^{3} - m^{3} n 2 m^{2} n^{2} 2 m^{2} n^{2} m^{4} + n^{4} - 2 m^{2} n^{2} m n^{3} - m^{3} n m^{3} n - m n^{3} 4 m^{2} n^{2} 4 m^{2} n^{2} - 4 m^{2} n^{2} (m^{2} - n^{2})^{2} 2 (m n^{3} - m^{3} n) - 2 (m n^{3} - m^{3} n) ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ Q_{11} Q_{22} Q_{12} Q_{66} ⎦ ⎥ ⎥ ⎥ ⎤ \overline{Q}_{i j} = \overline{Q}_{j i}

同理可得：

⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ \overline{S}_{11} \overline{S}_{21} \overline{S}_{61} \overline{S}_{12} \overline{S}_{22} \overline{S}_{62} \overline{S}_{16} \overline{S}_{26} \overline{S}_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ (3.2.2)

其中 $\overline{S}_{i j} (i, j = 1, 2, 6)$ 被称为偏轴柔量分量：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{S}_{11} \overline{S}_{22} \overline{S}_{12} \overline{S}_{66} \overline{S}_{16} \overline{S}_{26} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ m^{4} n^{4} m^{2} n^{2} 4 m^{2} n^{2} 2 m^{3} n 2 m n^{3} n^{4} m^{4} m^{2} n^{2} 4 m^{2} n^{2} - 2 m n^{3} - 2 m^{3} n 2 m^{2} n^{2} 2 m^{2} n^{2} m^{4} + n^{4} - 8 m^{2} n^{2} 2 (m n^{3} - m^{3} n) 2 (m n^{3} - m^{3} n) m^{2} n^{2} m^{2} n^{2} - m^{2} n^{2} (m^{2} - n^{2})^{2} m n^{3} - m^{3} n - m n^{3} + m^{3} n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ S_{11} S_{22} S_{12} S_{66} ⎦ ⎥ ⎥ ⎥ ⎤ \overline{S}_{i j} = \overline{S}_{j i}

偏轴模量矩阵和偏轴柔量矩阵互为逆矩阵。

3.3 单层的偏轴工程常数

3.3.1 偏轴工程常数定义

由于偏轴工程常数是表达偏轴下单轴应力或纯剪应力的刚度性能，因此可分别设：

σ_{x} \neq = 0, σ_{y} = τ_{x y} = 0; σ_{y} \neq = 0, σ_{x} = τ_{x y} = 0; τ_{x y} \neq = 0, σ_{x} = σ_{y} = 0

来定义偏轴工程常数。

例如在 $x y$ 平面内只有 $x$ 向正应力作用，即 $σ_{x} \neq = 0, σ_{y} = τ_{x y} = 0$ ，由 $(3.2.2)$ 得：

ϵ_{x}^{(x)} = \overline{S}_{11} σ_{x} ϵ_{y}^{(x)} = \overline{S}_{21} σ_{x} γ_{x y}^{(x)} = \overline{S}_{61} σ_{x}

定义 $x$ 轴向的拉压弹性模量：

E_{x} = \frac{σ _{x}}{ϵ _{x}^{(x)}}

泊松耦合系数：

ν_{x} \equiv ν_{y x} = - \frac{ϵ _{y}^{(x)}}{ϵ _{x}^{(x)}}

拉剪耦合系数：

η_{x y, x} = \frac{γ _{x y}^{(x)}}{ϵ _{x}^{(x)}}

这些弹性常数的前一个下标表示应力方向，后一个下标表示应变方向。

即可得到偏轴工程常数与柔量分量之间的关系：

E_{x} = \frac{1}{S _{11}}, ν_{x} = - \frac{S _{21}}{S _{11}}, η_{x y, x} = \frac{S _{61}}{S _{11}}

同理可得：

E_{y} = \frac{1}{S _{22}}, ν_{y} = - \frac{S _{12}}{S _{22}}, η_{x y, y} = \frac{S _{62}}{S _{22}} G_{x y} = \frac{1}{G _{66}}, η_{x, x y} = \frac{S _{16}}{S _{66}}, η_{y, x y} = \frac{S _{26}}{S _{66}}

其中 $G_{x y}$ 为剪切弹性模量。

或写作：

\overline{S}_{11} = \frac{1}{E _{x}}, \overline{S}_{12} = - \frac{ν _{y}}{E _{y}}, \overline{S}_{16} = \frac{η _{x, x y}}{G _{x y}} \overline{S}_{21} = - \frac{ν _{x}}{E _{x}}, \overline{S}_{22} = \frac{1}{E _{y}}, \overline{S}_{26} = \frac{η _{y, x y}}{G _{x y}} \overline{S}_{61} = \frac{η _{x y, x}}{E _{x}}, \overline{S}_{62} = \frac{η _{x y, y}}{E _{y}}, \overline{S}_{66} = \frac{1}{G _{x y}} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫

由于 $S_{i j} = S_{j i}$ ，偏轴工程弹性常数由具有如下性质：

\frac{ν _{x}}{ν _{y}} = \frac{E _{x}}{E _{y}} \frac{η _{x y, x}}{η _{x, x y}} = \frac{E _{x}}{G _{x y}} \frac{η _{x y, y}}{η _{y, x y}} = \frac{E _{y}}{G _{x y}} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫

3.3.2 偏轴工程弹性常数的转换关系

从上面的关系式可以看出工程弹性常数与柔量分量不能相互线性表示，所以偏轴工程弹性常数与正轴工程弹性常数之间不能得到矩阵的形式的转化公式。而只能用如下形式表示：

\frac{1}{E _{x}} = \frac{m ^{4}}{E _{L}} + \frac{n ^{4}}{E _{T}} + m^{2} n^{2} (\frac{1}{G _{L T}} - \frac{2 ν _{L}}{E _{L}}) \frac{1}{E _{y}} = \frac{m ^{4}}{E _{T}} + \frac{n ^{4}}{E _{L}} + m^{2} n^{2} (\frac{1}{G _{L T}} - \frac{2 ν _{L}}{E _{L}}) \frac{1}{G _{x y}} = \frac{m ^{4} + n ^{4}}{G _{L T}} + 2 m^{2} n^{2} (\frac{2}{E _{L}} + \frac{2}{E _{T}} + \frac{4 ν _{L}^{2}}{E _{L}} - \frac{1}{G _{L T}}) ν_{x} = E_{x} [(m^{4} + n^{4}) \frac{ν _{L}}{E _{L}} - m^{2} n^{2} (\frac{1}{E _{L}} + \frac{1}{E _{T}} - \frac{1}{G _{L T}})] ν_{y} = E_{y} [(m^{4} + n^{4}) \frac{ν _{L}}{E _{L}} - m^{2} n^{2} (\frac{1}{E _{L}} + \frac{1}{E _{T}} - \frac{1}{G _{L T}})] η_{x y, x} = E_{x} [m^{3} n (\frac{2}{E _{L}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}}) - m n^{3} (\frac{2}{E _{T}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}})] η_{x y, y} = E_{x} [m n^{3} (\frac{2}{E _{L}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}}) - m^{3} n (\frac{2}{E _{T}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}})] η_{x, x y} = G_{x y} [m^{3} n (\frac{2}{E _{L}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}}) - m n^{3} (\frac{2}{E _{T}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}})] η_{y, x y} = G_{x y} [m n^{3} (\frac{2}{E _{L}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}}) - m^{3} n (\frac{2}{E _{T}} + \frac{2 ν _{L}}{E _{L}} - \frac{1}{G _{L T}})] ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫

上述的偏轴工程弹性常数可以看作关于 $θ$ 的函数。弹性系数 $E_{x}$ 取极值的条件为：

\frac{d E _{x}}{d θ} = 0

解得：

s i n 2 θ = 0 c o s 2 θ = \frac{E _{L} - E _{T}}{E _{L} + E _{T} 2 E _{T} ν _{L} - \frac{E _{L} E _{T}}{G _{L T}}}

第一式表明 $θ = 0$ 时 $E_{x}$ 有极值，恰好等于 $E_{L}$ 和 $E_{T}$ ；第二式表明在非弹性主方向有极值的条件。由于 $∣ c o s 2 θ ∣ \leq 1$ 和 $E_{L} > E_{T}$ ，可得：

若
$G_{L T} > \frac{E _{L}}{2 ( 1 + ν _{L} )}$
$E_{x}$ 在非弹性主方向有极大值。
若
$G_{L T} < \frac{E _{T}}{2 ( 1 + ν _{T} )}$
$E_{x}$ 在非弹性主方向有极小值。
若
$\frac{E _{T}}{2 ( 1 + ν _{T} )} < G_{L T} < \frac{E _{L}}{2 ( 1 + ν _{L} )}$
$E_{x}$ 在非弹性主方向无极值。

目前所知的单向纤维增强材料均属于后两种情况。

4 单层的三维应力-应变关系

前面讨论单层刚度都是基于单层为平面应力状态下的应力-应变关系。本节讨论单层三维-应力应变关系，及它与平面应力状态下应力-应变关系的联系。

4.1 单层的一般三维应力-应变关系

如图所示，在弹性小变形的情况下，单层在任意符合右手螺旋的坐标系 $O x y z$ 下，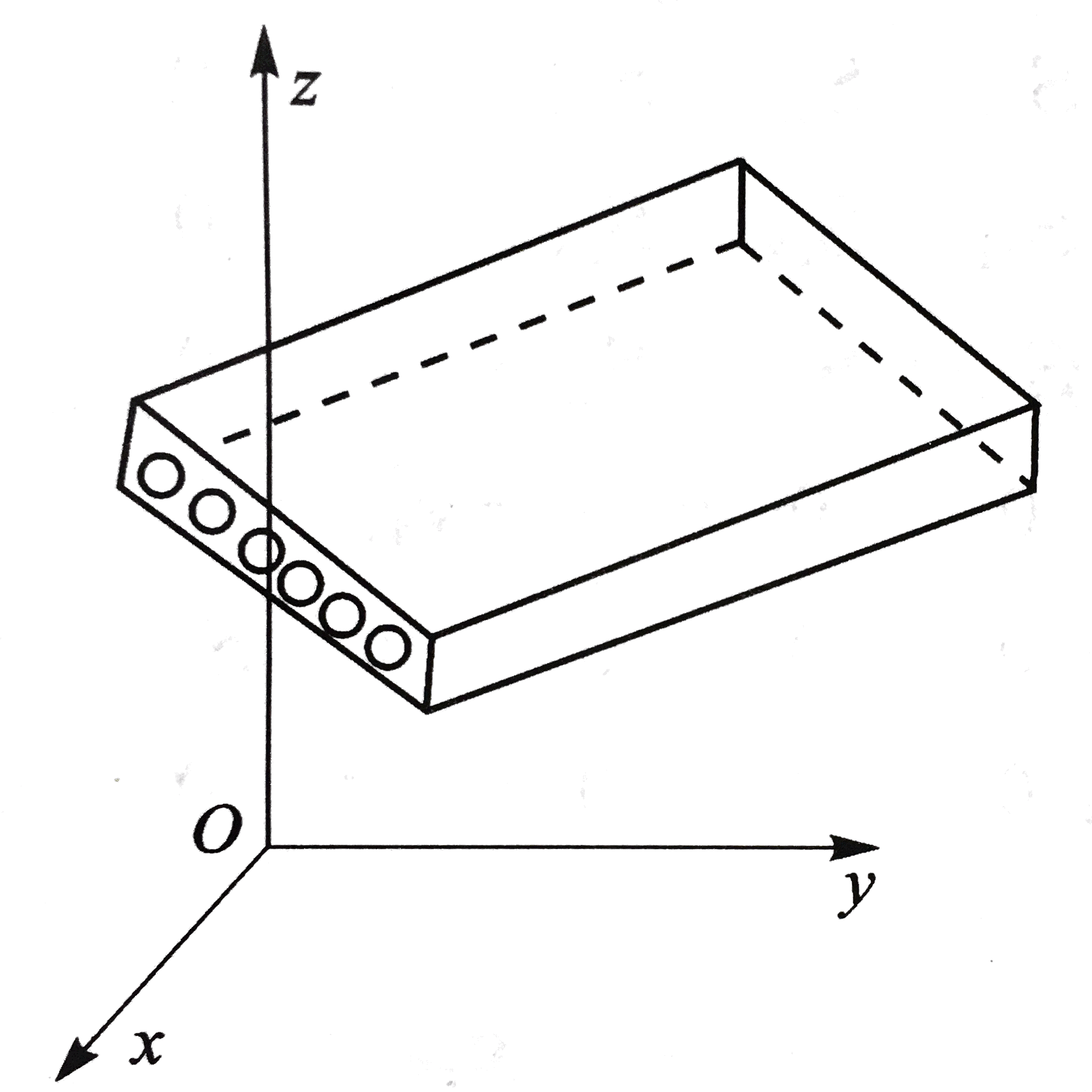
在正轴坐标系123下的单层
可以仿照平面应力状态下利用叠加原理得到应变-应力关系，推广到具有三维应力状态的情况，得到单层的一般三维应变-应力关系（广义胡克定律）为：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{S}_{11} \overline{S}_{21} \overline{S}_{31} \overline{S}_{41} \overline{S}_{51} \overline{S}_{61} \overline{S}_{12} \overline{S}_{22} \overline{S}_{32} \overline{S}_{42} \overline{S}_{52} \overline{S}_{62} \overline{S}_{13} \overline{S}_{23} \overline{S}_{33} \overline{S}_{43} \overline{S}_{53} \overline{S}_{63} \overline{S}_{14} \overline{S}_{24} \overline{S}_{34} \overline{S}_{44} \overline{S}_{54} \overline{S}_{64} \overline{S}_{15} \overline{S}_{25} \overline{S}_{35} \overline{S}_{45} \overline{S}_{55} \overline{S}_{65} \overline{S}_{16} \overline{S}_{26} \overline{S}_{36} \overline{S}_{46} \overline{S}_{56} \overline{S}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

或者简写成

\overline{ϵ} = \overline{S} \overline{σ} (4.1.1)

式中， $\overline{S}_{i j}$ 被称为三维柔量分量。

由 $(4.1.1)$ 可得单层的一般三维应力-应变关系式

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{C}_{11} \overline{C}_{21} \overline{C}_{31} \overline{C}_{41} \overline{C}_{51} \overline{C}_{61} \overline{C}_{12} \overline{C}_{22} \overline{C}_{32} \overline{C}_{42} \overline{C}_{52} \overline{C}_{62} \overline{C}_{13} \overline{C}_{23} \overline{C}_{33} \overline{C}_{43} \overline{C}_{53} \overline{C}_{63} \overline{C}_{14} \overline{C}_{24} \overline{C}_{34} \overline{C}_{44} \overline{C}_{54} \overline{C}_{64} \overline{C}_{15} \overline{C}_{25} \overline{C}_{35} \overline{C}_{45} \overline{C}_{55} \overline{C}_{65} \overline{C}_{16} \overline{C}_{26} \overline{C}_{36} \overline{C}_{46} \overline{C}_{56} \overline{C}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

或者简写成

\overline{σ} = \overline{C} \overline{ϵ} (4.1.2)

式中， $\overline{C}_{i j}$ 被称为三维模量分量。

且有

\overline{C}^{- 1} = \overline{S} \overline{C}_{i j} = \overline{C}_{j i} \overline{S}_{i j} = \overline{S}_{j i}

可见独立的弹性系数实际为21个。

4.2 单层的正轴三维应力-应变关系

如图所示，将单层至于正轴坐标系 $O x_{1} x_{2} x_{3}$ 上。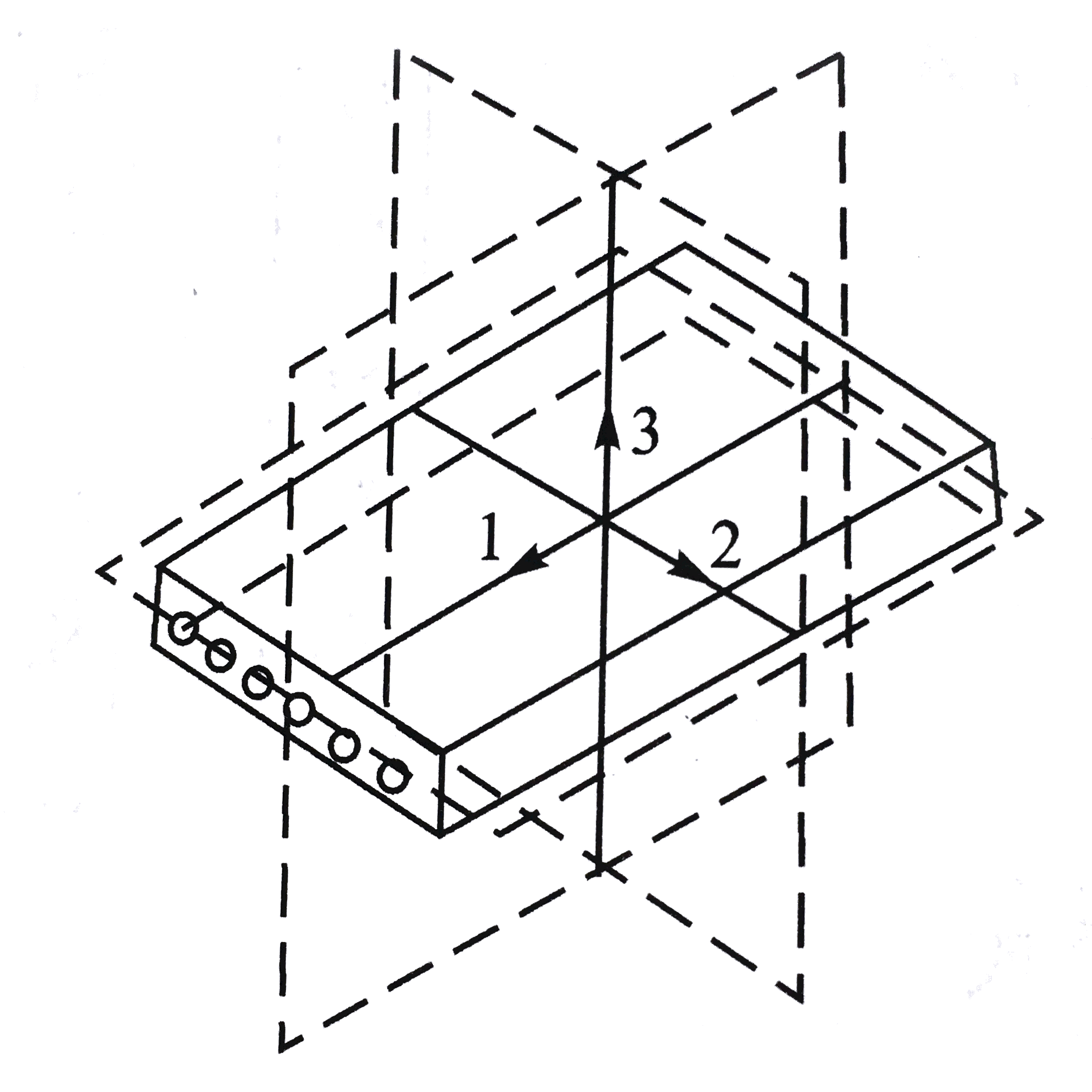
在正轴坐标系123下的单层
由于一点处的线应变 $ϵ_{1}$ 、 $ϵ_{2}$ 和 $ϵ_{3}$ 只与该点处的正应力 $σ_{1}$ 、 $σ_{2}$ 和 $σ_{3}$ 有关，同时该点处的剪应变 $γ_{23}$ 、 $γ_{31}$ 和 $γ_{12}$ 分别仅与剪应力 $τ_{23}$ 、 $τ_{31}$ 和 $τ_{12}$ 有关。所以单层正轴三维应力-应变关系式为：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{1} ϵ_{2} ϵ_{3} γ_{23} γ_{31} γ_{12} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ S_{11} S_{21} S_{31} 000 S_{12} S_{22} S_{32} 000 S_{13} S_{23} S_{33} 000 000 S_{44} 00 0000 S_{55} 0 00000 S_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{1} σ_{2} σ_{3} τ_{23} τ_{31} τ_{12} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

或者简写成

ϵ = S σ (4.2.1)

同样可得单层的正轴三维应力-应变关系式：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{1} σ_{2} σ_{3} τ_{23} τ_{31} τ_{12} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ C_{11} C_{21} C_{31} 000 C_{12} C_{22} C_{32} 000 C_{13} C_{23} C_{33} 000 000 C_{44} 00 0000 C_{55} 0 00000 C_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{1} ϵ_{2} ϵ_{3} γ_{23} γ_{31} γ_{12} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

或者简写成

σ = C ϵ (4.2.2)

且有

C^{- 1} = S C_{i j} = C_{j i} S_{i j} = S_{j i}

可见独立的正轴弹性系数为9个。

4.3 单层的偏轴三维应力-应变关系

可以证明，偏轴三维应变-应力关系式为：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{S}_{11} \overline{S}_{21} \overline{S}_{31} 00 \overline{S}_{61} \overline{S}_{12} \overline{S}_{22} \overline{S}_{32} 00 \overline{S}_{62} \overline{S}_{13} \overline{S}_{23} \overline{S}_{33} 00 \overline{S}_{63} 000 \overline{S}_{44} \overline{S}_{54} 0 000 \overline{S}_{45} \overline{S}_{55} 0 \overline{S}_{16} \overline{S}_{26} \overline{S}_{36} 00 \overline{S}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

偏轴三维应力-应变关系式为：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{C}_{11} \overline{C}_{21} \overline{C}_{31} 00 \overline{C}_{61} \overline{C}_{12} \overline{C}_{22} \overline{C}_{32} 00 \overline{C}_{62} \overline{C}_{13} \overline{C}_{23} \overline{C}_{33} 00 \overline{C}_{63} 000 \overline{C}_{44} \overline{C}_{54} 0 000 \overline{C}_{45} \overline{C}_{55} 0 \overline{C}_{16} \overline{C}_{26} \overline{C}_{36} 00 \overline{C}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

且有

\overline{C}^{- 1} = \overline{S} \overline{C}_{i j} = \overline{C}_{j i} \overline{S}_{i j} = \overline{S}_{j i}

可见正交各向异性的单层偏轴三维弹性系数为13个。可以证明，正交各向异性的单层三维独立的弹性系数与正交三维弹性系数一样，为9个。

4.4 与平面应力状态的关系

观察偏轴三维应变-应力关系式和偏轴平面应力状态应变-应力关系式：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{S}_{11} \overline{S}_{21} \overline{S}_{31} 00 \overline{S}_{61} \overline{S}_{12} \overline{S}_{22} \overline{S}_{32} 00 \overline{S}_{62} \overline{S}_{13} \overline{S}_{23} \overline{S}_{33} 00 \overline{S}_{63} 000 \overline{S}_{44} \overline{S}_{54} 0 000 \overline{S}_{45} \overline{S}_{55} 0 \overline{S}_{16} \overline{S}_{26} \overline{S}_{36} 00 \overline{S}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ \overline{S}_{11} \overline{S}_{21} \overline{S}_{61} \overline{S}_{12} \overline{S}_{22} \overline{S}_{62} \overline{S}_{16} \overline{S}_{26} \overline{S}_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤

前一个等式是后一个等式的推广。
对于平面应力状态， $σ_{z} = τ_{y z} = τ_{x z} = 0$ 。于是可删去前一个等式中的应力矢量 $σ$ 的第三、四和五行，以及柔量矩阵 $\overline{S}$ 的第三、四和五列。同时，由于不关心 $ϵ_{z}$ 、 $γ_{y z}$ 和 $γ_{z x}$ 三个量，可以删去前一个等式中的应变矢量 $ϵ$ 的第三、四和五行，以及柔量矩阵 $\overline{S}$ 的第三、四和五行。则第一式变为第二式。

可见平面应力状态的柔量分量和偏轴三维状态的柔量分量对应相等。对于一般三维应力状态和平面应力状态也有一样的关系。

观察偏轴三维应力-应变关系式和偏轴平面应力状态应力-应变关系式：

⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{y z} τ_{z x} τ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{C}_{11} \overline{C}_{21} \overline{C}_{31} 00 \overline{C}_{61} \overline{C}_{12} \overline{C}_{22} \overline{C}_{32} 00 \overline{C}_{62} \overline{C}_{13} \overline{C}_{23} \overline{C}_{33} 00 \overline{C}_{63} 000 \overline{C}_{44} \overline{C}_{54} 0 000 \overline{C}_{45} \overline{C}_{55} 0 \overline{C}_{16} \overline{C}_{26} \overline{C}_{36} 00 \overline{C}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{y z} γ_{z x} γ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ \overline{Q}_{11} \overline{Q}_{21} \overline{Q}_{61} \overline{Q}_{12} \overline{Q}_{22} \overline{Q}_{62} \overline{Q}_{16} \overline{Q}_{26} \overline{Q}_{66} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} ⎦ ⎥ ⎤

对于平面应力状态， $σ_{z} = τ_{y z} = τ_{x z} = 0$ 。于是可删去前一个等式中的应力矢量 $σ$ 的第三、四和五行，以及模量矩阵 $\overline{C}$ 的第三、四和五行。若想要删去应变矢量 $ϵ$ 第三、四和五行，需要将应变矢量 $ϵ$ 中的 $ϵ_{z}$ 、 $γ_{y z}$ 和 $γ_{z x}$ 三个量的影响折合到其它量中。
由于 $σ_{z} = 0$ ，则由前一个矩阵方程得：

σ_{z} = \overline{C}_{31} ϵ_{x} + \overline{C}_{32} ϵ_{y} + \overline{C}_{33} ϵ_{z} + \overline{C}_{36} γ_{x y} = 0

所以：

ϵ_{z} = - \frac{1}{C _{33}} (\overline{C}_{31} ϵ_{x} + \overline{C}_{32} ϵ_{y} + \overline{C}_{36} γ_{x y})

代入到前一个矩阵方程中的 $σ_{x}$ 部分得：

σ_{x} = (\overline{C}_{11} - \frac{C _{13}^{2}}{C _{33}}) ϵ_{x} + (\overline{C}_{12} - \frac{C _{13} C _{23}}{C _{33}}) ϵ_{y} + (\overline{C}_{16} - \frac{C _{13} C _{63}}{C _{33}}) γ_{x y}

由后一个矩阵方程的 $σ_{x}$ 部分得：

σ_{x} = \overline{Q}_{11} ϵ_{x} + \overline{Q}_{12} ϵ_{y} + \overline{Q}_{16} γ_{x y}

于是：

\overline{Q}_{11} = \overline{C}_{11} - \frac{C _{13}^{2}}{C _{33}}, \overline{Q}_{12} = \overline{C}_{12} - \frac{C _{13} C _{23}}{C _{33}}, \overline{Q}_{16} = \overline{C}_{16} - \frac{C _{13} C _{63}}{C _{33}}

同理由前一个和后一个矩阵方程的 $σ_{y}$ 和 $τ_{x y}$ 部分，综合可得：

\overline{Q}_{i j} = \overline{C}_{i j} - \frac{C _{i 3} C _{j 3}}{C _{33}} (i, j = 1, 2, 6)

于是在前面的基础上，将前一个矩阵方程的应变矢量 $ϵ$ 第三、四和五行和模量矩阵 $\overline{C}$ 的第三、四和五列删去。并利用上式将 $\overline{C}_{i j}$ 换成 $\overline{Q}_{i j}$ 。则前一个矩阵方程变为后一个矩方程。

可见平面应力状态的模量分量和偏轴三维状态的模量分量是不同的。对于一般三维应力状态和平面应力状态也有类似的关系。

4.5 单层的三维工程弹性常数

单层的三维工程常数是单层在三维情况下，由单轴应力与纯剪应力确定的刚度性能参数。以单层的正轴情况为例，在 $(4.2.1)$ 中分别设6个应力分量不为零，其余分量均为零来定义。

例如，设 $σ_{1} \neq = 0, σ_{2} = σ_{3} = τ_{23} = τ_{13} = τ_{12} = 0$ ，可得：

ϵ_{1}^{(1)} = S_{11} σ_{1} ϵ_{2}^{(1)} = S_{12} σ_{1} ϵ_{3}^{(1)} = S_{13} σ_{1} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫

定义主方向1轴向的拉压弹性模量：

E_{1} = \frac{σ _{1}}{ϵ _{1}^{(1)}}

泊松耦合系数：

ν_{21} = - \frac{ϵ _{2}^{(1)}}{ϵ _{1}^{(1)}} ν_{31} = - \frac{ϵ _{3}^{(1)}}{ϵ _{1}^{(1)}} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫

于是可得三维正轴工程常数与柔量分量之间的关系：

E_{1} = \frac{1}{S _{11}} ν_{21} = - \frac{S _{21}}{S _{11}} ν_{31} = - \frac{S _{31}}{S _{11}} ⎭ ⎪ ⎬ ⎪ ⎫

同理可得：

E_{2} = \frac{1}{S _{22}} ν_{12} = - \frac{S _{12}}{S _{22}} ν_{31} = - \frac{S _{32}}{S _{22}} ⎭ ⎪ ⎬ ⎪ ⎫ E_{3} = \frac{1}{S _{33}} ν_{13} = - \frac{S _{13}}{S _{33}} ν_{23} = - \frac{S _{23}}{S _{33}} ⎭ ⎪ ⎬ ⎪ ⎫ G_{23} = \frac{1}{S _{44}} G_{31} = \frac{1}{S _{55}} G_{12} = \frac{1}{S _{66}} ⎭ ⎪ ⎬ ⎪ ⎫

由于 $S_{i j} = S_{j i}$ ：

\frac{ν _{i j}}{ν _{j i}} = \frac{E _{i}}{E _{j}} (i, j = 1, 2, 3)

5 单层板的强度

5.1 单层板的强度指标

各向异性的单层板强度指标需给出5个基本强度，即：
$X_{t}$ ——单层板纵向拉伸强度；
$X_{c}$ ——单层板纵向压缩强度；
$Y_{t}$ ——单层板横向拉伸强度；
$Y_{c}$ ——单层板横向压缩强度；
$S$ ——单层板面内剪切强度。
同弹性系数一样，强度指标也由单层板的拉伸、压缩和剪切试验确定。单层板5个强度指标与4个工程弹性系数一起合称为复合材料单层板的九参数。

5.2 单层板的失效准则

设单层板位于正轴坐标系 $O x_{1} x_{2} x_{3}$ 下。应力应变下标中的123表示其方向沿正轴坐标 $O x_{1} x_{2} x_{3}$ 的坐标轴。不要与材料力学中各向同性材料的主应力主应变方向混淆。

5.2.1 最大应力理论

单层的最大应力准则认为，复合材料在复杂应力状态下进入破坏是由于其中某个应力分量达到了材料的基本强度值。其判据式为：

σ_{1} = X_{t} （ 或 ∣ σ_{1} ∣ = X_{c} ） σ_{2} = Y_{t} （ 或 ∣ σ_{2} ∣ = Y_{c} ） ∣ τ_{12} ∣ = S ⎭ ⎪ ⎬ ⎪ ⎫ (5.2.1.1)

这三个表达式各自独立，未考虑各应力分量与材料强度的相互影响。只要有一个左边等于或大于右边的值，则认为材料已经失效。

5.2.2 最大应变理论

单层的最大应变准则认为，复合材料在复杂应力状态下进入破坏的主要原因，是材料正轴方向的应变值达到了各基本强度值所对应的应变值。其判据式为：

ϵ_{1} = ϵ_{X_{t}} （ 或 ∣ ϵ_{1} ∣ = ϵ_{X_{c}} ） ϵ_{2} = ϵ_{Y_{t}} （ 或 ∣ ϵ_{2} ∣ = ϵ_{Y_{c}} ） ∣ γ_{12} ∣ = γ_{S} ⎭ ⎪ ⎬ ⎪ ⎫

由于上式中的极限应变是与单轴应力或纯剪切应力状态下基本强度对应的，而材料失效是线弹性的，故

ϵ_{X_{t}} = \frac{X _{t}}{E _{L}}, ϵ_{X_{c}} = \frac{X _{c}}{E _{L}} ϵ_{Y_{t}} = \frac{Y _{t}}{E _{T}}, ϵ_{Y_{c}} = \frac{Y _{c}}{E _{T}} γ_{S} = \frac{S}{G _{L T}} ⎭ ⎪ ⎬ ⎪ ⎫

于是得：

σ_{1} - ν_{L} σ_{2} = X_{t} （ 或 ∣ σ_{1} - ν_{L} σ_{2} ∣ = X_{c} ） σ_{2} - ν_{T} σ_{2} = Y_{t} （ 或 ∣ σ_{2} - ν_{T} σ_{2} ∣ = Y_{c} ） ∣ τ_{12} ∣ = S ⎭ ⎪ ⎬ ⎪ ⎫ (5.2.2.1)

最大应变准则也是由3个互不影响、各自独立的表达式组成。只要满足上式中的一个，就意味着单层板被破环。

5.2.3 蔡-希尔（Tsai-Hill）理论与霍夫曼（Hoffman）理论

蔡-希尔从各向同性材料的畸变能强度理论出发，提出了单层板的蔡-希尔失效准则。其一般形式为：

F (σ_{2} - σ_{3})^{2} + G (σ_{3} - σ_{1})^{2} + H (σ_{1} - σ_{2})^{2} + 2 L τ_{23}^{2} + 2 M τ_{31}^{2} + 2 N τ_{12}^{2} = 1

系数F、G、H、L、M、N由单层板的拉、压和纯剪切实验确定。

如，单层板仅有 $τ_{12}$ 作用时， $(τ_{12})_{m a x} = S$ ，代入上式，得：

N = \frac{1}{2 S ^{2}}

同样，当单层板分别仅有 $σ_{1}$ 、 $σ_{2}$ 、 $σ_{3}$ 作用时，可分别得到：

G + H = \frac{1}{X ^{2}} F + H = \frac{1}{Y ^{2}} F + G = \frac{1}{Z ^{2}} ⎭ ⎪ ⎬ ⎪ ⎫

$X$ 、 $Y$ 、 $Z$ 分别为主轴坐标系三个方向的强度（拉伸或者压缩），对于纤维增强板， $Y \approx Z$ ，由上述三个式子，可以得到：

G = H = \frac{1}{2 X ^{2}} F = \frac{1}{Y ^{2}} - \frac{1}{2 X ^{2}}}

对于平面应力状态， $σ_{z} = τ_{y z} = τ_{x z} = 0$ ，蔡-希尔准则变为：

(\frac{σ _{1}}{X})^{2} + (\frac{σ _{2}}{Y})^{2} - \frac{σ _{1} σ _{2}}{X ^{2}} + (\frac{τ _{12}}{S})^{2} = 1 (5.2.3.1)

蔡-希尔理论未考虑拉伸、压缩强度不一致的影响。一般情况下，使用蔡-希尔理论，在结构承受拉伸载荷时，使用拉伸强度；压缩时，使用压缩强度。

Hoffman分析了单层板拉压强度不相同的这一因素，在蔡-希尔理论中补充了几个一次项，即：

C_{1} (σ_{1} - σ_{2})^{2} + C_{2} (σ_{3} - σ_{1})^{2} + C_{3} (σ_{2} - σ_{3})^{2} + C_{4} σ_{1} + C_{5} σ_{2} + C_{6} σ_{3} + C_{7} τ_{23}^{2} + C_{8} τ_{31}^{2} + C_{9} τ_{12}^{2} = 1

其平面应力状态下的失效准则为：

\frac{σ _{1}^{2} - σ _{1} σ _{2}}{X _{t} X _{c}} + \frac{σ _{2}^{2}}{Y _{t} Y _{c}} + \frac{X _{c} - X _{t}}{X _{t} X _{c}} σ_{1} + \frac{Y _{c} - Y _{t}}{Y _{t} Y _{c}} σ_{2} + \frac{τ _{12}^{2}}{S ^{2}} = 1 (5.2.3.2)

5.2.4 蔡-胡失效准则

对于单层板，蔡-胡失效准则为：

F_{11} σ_{1}^{2} + 2 F_{12} σ_{1} σ_{2} + F_{22} σ_{2}^{2} + F_{66} σ_{6}^{2} + F_{1} σ_{1} + F_{2} σ_{2} = 1 (5.2.4.1)

其中：

F_{11} = \frac{1}{X _{t} X _{c}}, F_{22} = \frac{1}{Y _{t} Y _{c}}, F_{66} = \frac{1}{S ^{2}} F_{1} = \frac{1}{X _{t}} - \frac{1}{X _{c}}, F_{2} = \frac{1}{Y _{t}} - \frac{1}{Y _{c}}, σ_{6} = τ_{12}}

另外， $F_{12}$ 应包含 $σ_{1}$ 、 $σ_{2}$ 的双轴试验测得，但一般可采用：

\[F_{12}=-\frac{1}{2}\sqrt{F_{11}F_{22}}\]

若设 2 F_{12} = - F_{11} ，则蔡-胡失效准则等同于Hoffman失效准则；若 2 F_{12} = - \frac{1}{X ^{2}} ，则蔡-胡失效准则等同于蔡-希尔失效准则。

5.3 单层板的强度比方程

为了定量说明单层板在不失效时的安全裕度，引进强度/应力比，简称强度比，使失效准则表达式变成强度比方程，对于给定的作用应力分量，能定量地给出它的安全裕度。

单层在作用应力作用下，极限应力的某一个分量与其对应的作用应力分量之比称为强度/应力比，简称强度比，记为 $R$

R = \frac{σ _{i (a)}}{σ _{i}} (5.3.1)

式中， $σ_{i}$ 为作用的应力分量， $σ_{i (a)}$ 为对应于 $σ_{i}$ 的极限应力分量。
这里的“对应”的含义是基于假设 $σ_{i} (i = 1, 2, 3)$ 为比例加载的。因此，对于任何应力分量，强度比值是相同的。

$R$ 的含义：
$R = \infty$ ：作用力 $σ_{i} = 0$ ;
$∣ R ∣ > 1$ ：结构安全， $R - 1$ 为作用力达到单层板失效时尚可增加的应力倍数；
$∣ R ∣ = 1$ ：作用应力正好达到结构极限应力值；
$∣ R ∣ < 1$ ：结构已经失效，无实际意义。在设计计算中表明结构强度不够。

将强度比 $(5.3.1)$ 代入强度理论可以得到强度比方程。如蔡-希尔失效判据的强度比方程为：

A R^{2} = 1 A = (\frac{σ _{1}}{X})^{2} + (\frac{σ _{2}}{Y})^{2} - \frac{σ _{1} σ _{2}}{X ^{2}} + (\frac{τ _{12}}{S})^{2}

则：

∣ R ∣ = \frac{1}{A} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ > 1 安 全 ， 其 值 为 安 全 裕 度 = 1 临 界 破 坏 状 态 < 1 材 料 已 被 破 坏

6 总结

纤维增强复合材料的单层的材料属性是各向异性的，所以描述其性能参数以及应力应变都必须以矩阵（矢量）表示。
正轴刚度是通过实验测得的，通常其他坐标系的参数都可以用正轴刚度参数表示出来。
复合材料的强度理论是各向同性材料力学强度理论的推广。
复合材料力学除了研究单层的性质，也会研究层合板的属性。

本文章使用limfx的vsocde插件快速发布