Kirchhoff假设下的薄板弯曲

回到主页

本文为学习笔记,只记录重点内容,详细过程自行查找资料

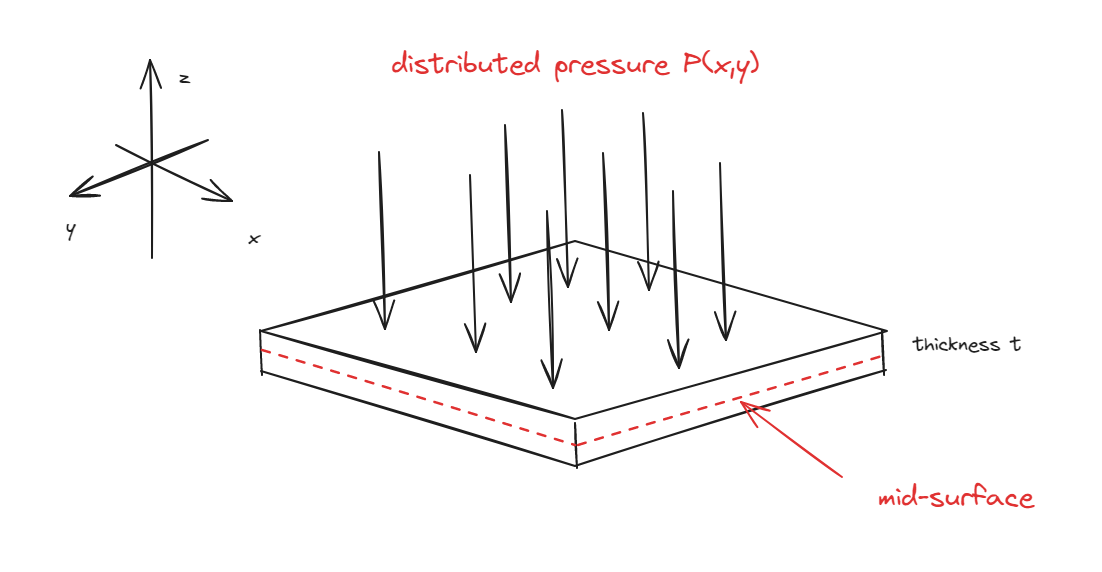
1. 问题描述

对于长厚比比较大的薄板,在厚度方向收到分布的垂直载荷p(x,y),要求板的形变及应力.

p(x,y)也可以称为横向载荷

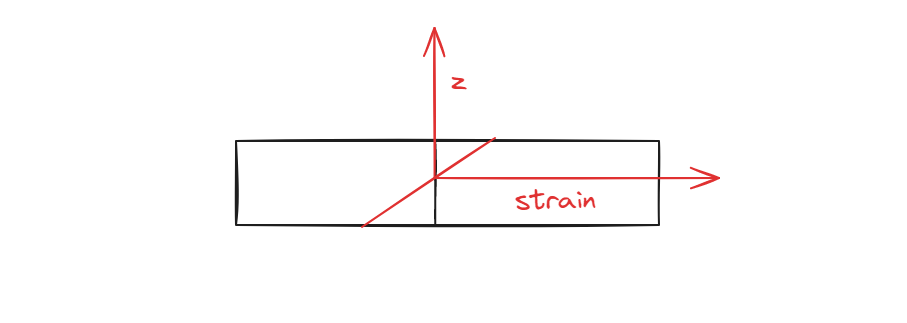
alt text

2. Kirchhoff假设

提出了如下假设:

  1. 厚度正应变为0;

  2. 产生的应变不计;

  3. 中面各点不产生面内位移,即;

进一步,上述假设可以表述为:

\epsilon _z=0
\\
\gamma _{yz}=\gamma _{xz}=0
\\
w=w\left( x,y \right) 
\\
u=-\frac{\partial w}{\partial x}z
\\
v=-\frac{\partial w}{\partial y}z

由上可定义位移向量为:

\vec{u}=\{u, v, w\}=\{-\frac{\partial w}{\partial x}z,-\frac{\partial w}{\partial y}z ,w(x,y)\}^T

根据应变定义有:

\epsilon =\left\{ \epsilon _x,\epsilon _y,\gamma _{xy} \right\} ^T=\left\{ -\frac{\partial \boldsymbol{w}^2}{\partial x^2}z,-\frac{\partial \boldsymbol{w}^2}{\partial y^2}z,-2\frac{\partial \boldsymbol{w}^2}{\partial x\partial y}z \right\} ^T

根据转角为挠度一阶导数的定义可知:

\theta _x=\frac{\partial w}{\partial y}

\theta _y=-\frac{\partial w}{\partial x}

进一步,曲率和扭曲率的定义为:

\chi _x=\frac{\partial \theta _y}{\partial x}=-\frac{\partial \boldsymbol{w}^2}{\partial x^2}
\\
\chi _y=-\frac{\partial \theta _x}{\partial y}=-\frac{\partial \boldsymbol{w}^2}{\partial y^2}\\
\chi _{xy}=0.5\left( \frac{\partial \theta _y}{\partial y}-\frac{\partial \theta _x}{\partial x} \right) =-\frac{\partial \boldsymbol{w}^2}{\partial x\partial y}

从医上可以就看出,应变和应力都可以用扭曲率来表示:

\left\{ \epsilon _x,\epsilon _y,\gamma _{xy} \right\} ^T=\left\{ \chi _xz,\chi _yz,2\chi _{xy}z \right\} ^T

\sigma _x=\frac{Ez}{1-\nu ^2}\left( \chi _x+\nu \chi _y \right) 
\\
\sigma _y=\frac{Ez}{1-\nu ^2}\left( \chi _y+\nu \chi _x \right) 
\\
\tau _{xy}=\frac{Ez}{2\left( 1+\nu \right)}\chi _{xy}

alt text

再进一步,根据应力在厚度上的积分,可以计算得到薄板力矩向量(合力):

\vec{M}=\left\{ \begin{array}{c}
	\int_{-0.5t}^{-0.5t}{\sigma _xzdz}\\
	\begin{array}{c}
	\int_{-0.5t}^{-0.5t}{\sigma _yzdz}\\
	\int_{-0.5t}^{-0.5t}{\sigma _{xy}zdz}\\
\end{array}\\
\end{array} \right\} =D\left\{ \begin{array}{c}
	\begin{array}{c}
	\chi _x\\
	\chi _y\\
\end{array}\\
	\chi _{xy}\\
\end{array} \right\} ,there: D=\frac{Et^3}{12\left( 1-\nu ^2 \right)}\left( \begin{matrix}
	1&		\nu&		\\
	\nu&		1&		\\
	&		&		\frac{1-\nu}{2}\\
\end{matrix} \right)

此时,薄板单元的总势能(应变能-外力做的功)可以表示为:

\varPi _e=\frac{1}{2}\int_A{M^T}\left\{ \begin{array}{c}
	\begin{array}{c}
	\chi _x\\
	\chi _y\\
\end{array}\\
	\chi _{xy}\\
\end{array} \right\} dA-\int_A{p\left( x,y \right)}w\left( x,y \right) dA
\\
=\frac{1}{2}\int_A{\left\{ \begin{array}{c}
	\begin{array}{c}
	\chi _x\\
	\chi _y\\
\end{array}\\
	\chi _{xy}\\
\end{array} \right\} ^TD^T}\left\{ \begin{array}{c}
	\begin{array}{c}
	\chi _x\\
	\chi _y\\
\end{array}\\
	\chi _{xy}\\
\end{array} \right\} dA-\int_A{p\left( x,y \right)}w\left( x,y \right) dA

根据以上推导,薄板单元的刚度矩阵Ke是可以求出的.

本文章使用limfx的vscode插件快速发布