5 涡流场数值模拟
==============
5.1 基本理论
5.1.1时谐场量的向量表示
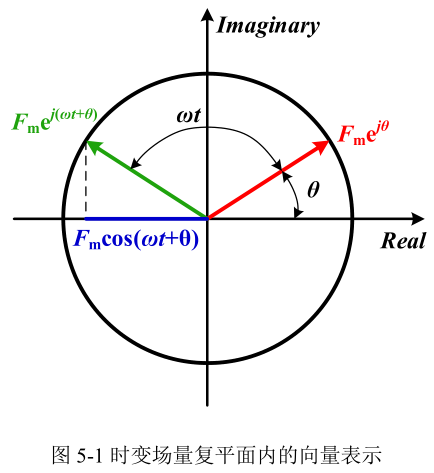
在时谐场中,场量不仅是空间的函数,还是时间的函数,且在时间上按正弦函数变化。如果将场量表示为复平面内的向量,则场量的表示与时间无关,可以极大的简化时谐场的分析。因此,在时谐场中,所有的场量均按向量的形式表示,在Maxwell的涡流场(亦称为"时谐场")分析中,所有的场量也都是以向量的形式表示。下面对时谐场量的向量表示做简单的介绍。
基于欧拉公式ejα=cosα+jsinα,对于任意随时间按正弦函数变化的场量可表示为
\[ \begin{aligned} F(t) &=F_{m} \cos (\omega t+\theta) \\ &=\operatorname{Re}\left\{F_{m}[\cos (\omega t+\theta)+j \sin (\omega t+\theta)]\right\} \\ &=\operatorname{Re}\left[F_{m} e^{j(\omega+\theta)}\right] \end{aligned} \]
由上式可知,任何随时间正弦变化的场量F(t)=Fmcos(ωt+θ)均可以表示为复数Fmejθejωt的实部,其中Fm为场量的幅值,θ为F(t)的初始相位,ω为角频率。需要注意的是,在Maxwell时谐场分析中,所有场量具有相同的角频率。Fmejθejωt包含两部分,Fmejθ表示复平面内相位为θ的固定向量(如图5‑1中红色线段所示),ejωt表示固定向量Fmejθ在复平面内的旋转角,F(t)=Fmcos(ωt+θ)就可以视为Fmejθejωt在实轴上的投影(如图5‑1中蓝色线段所示)。
5.1.2时谐电磁场方程
在Maxwell的时谐场求解中,一般将求解域分为导体区域和非导体区域分别求解。导体区域的电磁场方程可以通过时谐Maxwell方程推导得到,首先将Maxwell方程改写为时谐场形式,只需将将Maxwell方程中的时间偏微分∂/∂t替换为jω即可,即
\[ \begin{array}{l}\nabla \times \boldsymbol{E}=-j \omega \boldsymbol{B} \\ \nabla \times \frac{1}{\mu} \boldsymbol{B}=\boldsymbol{J}+j \omega \varepsilon \boldsymbol{E} \\ \nabla \cdot \boldsymbol{E}=\rho / \varepsilon \\ \nabla \cdot \boldsymbol{B}=0\end{array} \]
在Maxwell涡流场求解器中,实际求解变量是矢量磁位A,其定义为
\[ \begin{array}{l} \nabla \times \boldsymbol{E}=-j \end{array} \]
结合物性方程J=σE,可得
\[ \nabla \times \frac{1}{\mu}(\nabla \times \boldsymbol{A})=(\sigma+j \omega \varepsilon) \boldsymbol{E} \]
当采用矢量磁位A时,电场可表示为
\[ \boldsymbol{E}=-j \omega \boldsymbol{A}-\nabla \varphi \]
其中,φ为电位,由式(5-4)和式(5-5)可得
\[ \nabla \times \frac{1}{\mu}(\nabla \times \boldsymbol{A})=(-j \omega \boldsymbol{A}-\nabla \varphi)(\sigma+j \omega \varepsilon) \]
式即为Maxwell涡流场求解器中导体区域的方程,主要求解变量为矢量磁位A和标量电位φ。根据相关边界条件,对式进行求解,即可得到矢量磁位A和标量电位φ,进而可以计算出其他的物理量。
对于非导体区域,电流密度为0,忽略位移电流,则∇×B=0,即非导体区域的磁场可认为是无旋场,可以采用类似于静电场中的标量位进行求解。在Maxwell中,非导体区域求解的是标量磁位φm的拉普拉斯方程,即
\[ \nabla \cdot\left(\mu \nabla \varphi_{m}\right)=0 \]
式(5-6)右端为电流密度,包含三个分量,即Js=-σ∇φ为导体电势梯度产生的源电流密度;Je=-jωσA为由时变磁场产生的感应电流密度;Jd=-jωε(jωA+∇φ)为时变电场产生的位移电流,对于低频场而言,位移电流一般可以忽略。以上具体内容有兴趣的同学可以参考电磁场相关书籍。
5.2 主要前处理方法
在时谐场分析中,相关的激励源与边界条件和静磁场分析类似,下面简单介绍一下Maxwell中与时谐场相关的激励源、边界条件及其他前处理方法。
5.2.1激励源
电流密度(Current Density Excitation)
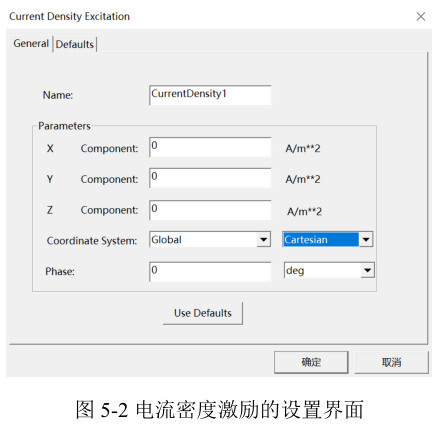
如果已知导体内的电流密度分布,则可施加电流密度分布载荷,这是一种非常强的约束。电流密度激励在2D和3D分析中均可施加。在2D分析中,电流密度只有垂直于分析平面方向上的分量:在2D平面(无限长直模型,XY平面)坐标系中,电流密度只存在Z分量;在2D轴对称(圆柱模型,RZ平面)坐标系中,电流密度只存在环向(θ,在模型中显示为Y)分量。在3D模型中,电流密度激励施加在3D实体中,可以分别设置设置X、Y、Z三个方向的电流密度。3D分析中的电流密度激励具体设置界面如图5‑2所示,在坐标系选项栏可以选择笛卡尔坐标系、圆柱坐标系、球坐标系,用于定义更复杂的电流密度分布,具体用法与静磁场分析中讲到的材料坐标系相同。
电流密度终端(Current Density Terminal Excitation)
在3D分析中,电流密度激励需要与电流密度终端联合使用,这个激励主要是让软件识别施加的电流回路。在闭合导体中,只需在与电流传导方向垂直的截面上施加电流密度终端即可;在开路导体中,需要在导体在求解域的端面施加电流密度终端。需要注意的是,由于电流散度必须为零(电流必须构成闭合回路),在建模时开路导体的两个端面必须在求解域的边界上,这时可以认为电流从无穷远处返回。
电流激励(Current Excitation)
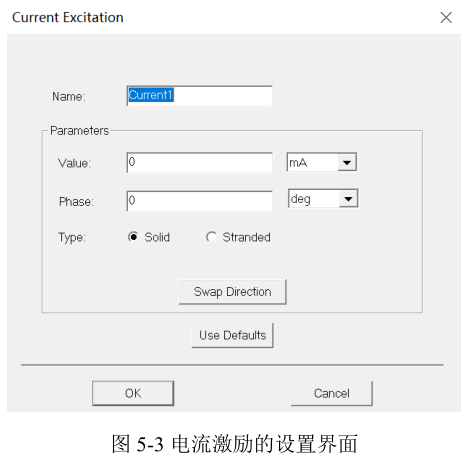
如果已知导体上的总电流,则可以施加电流激励,这也是一个相对较强的激励。电流激励的施加方法与电流密度终端的施加方法类似,与静磁场分析里的电流激励也相同。图5‑3所示为电流激励设置界面,除设置导体总电流外,还需要设置电流的相位。在类型选项卡中,可以选择Solid和Stranded:其中Solid表示实心导体,在涡流分析中一般需要考虑趋肤效应,需要与"设置涡流效应"(Set Eddy Effect)配合使用;Stranded表示由多个相互绝缘的细导线绞合而成的绞线导体,且每根导线的电流相同,即可认为电流在模型截面上是平均分布的,不需要考虑趋肤效应。
线圈终端激励(Coil Terminal Excitation)
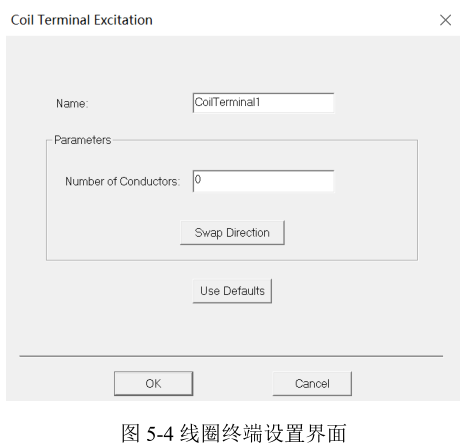
在Maxwell中可以将载流导体定义为线圈,再施加载荷,线圈终端激励主要用于确定线圈的电流路径。对于闭合导体,可以在导体上任意与电流方向垂直的截面上定义线圈终端;对于开路导体,需要在导体的两个端面定义线圈终端,且导体端面必须与求解域的边界重合。图5‑4所示为线圈终端激励设置界面,其中只需要设置导体数:对于实心导体(相当于电流激励里的Solid类型),导体数应设置为1;对于绞合导体(相当于电流激励里的Stranded类型),导体数应按模型中实际导线数设置。如果因利用对称性将模型进行了分割,只需要填写分割后的模型包含的实际导体数。
绕组设置(Winding Setup)
在线圈终端激励中,只设置了导体数,并没有设置具体的载荷,其载荷的设置需要用到绕组设置。一般而言,对一个实体模型可设置一个线圈终端,而一个绕组内可以添加多个相同激励的线圈。在电机、变压器等三相设备的仿真中,一般将每一相定义为一个绕组,将该相内所有线圈全部添加到该绕组内。可以将绕组理解为线圈组,而线圈是其下的组员。
绕组可以用来设置多种类型的激励,包括电流激励、电压激励和外部电路激励。图5‑5所示为绕组设置界面,在类型选项卡中可以选择激励类型:对于电流型激励,需要设计电流大小及电流相位;对于电压型激励,需要设计电压大小、电压相位、电阻及电感;对于外部电路激励,无需设置,但需要设置相关的外部电路,具体参见"外部电路设置"部分。
需要注意的是,在电压型激励中,不同类型绕组设置的电阻的含义不同。对于实心绕组(Solid),绕组本身的电阻程序会自动计算,设置的电阻为绕组之外的电阻,包括线路电阻、电源内阻等。对于绞合绕组(Stranded),绕组本身的电阻程序不会自动计算,设置的电阻除线路电路、电源内阻等外部电阻之外,还应包括绕组本身的电阻。对于实体绕组和绕线式绕组,程序会自动计算器电感,所设置的电感均为绕组之外的电感,如线路电感。
外部电路(External Circuit)
有时候载荷是通过外部电路驱动的,这时需要用到外部电路激励。只有在绕组中才能施加外部电路激励。由于涡流场是频域求解器,在电路中只支持线性元件,如电感、电阻、电容、变压器,激励类型也必须是正弦激励,如正弦的电压源和电流源。
平行电流激励(Parallel Current Excitation)
在有些分析中,有时候知道多个并联导体的总电流,但不知道电流在各个导体中的分布,这个时候就可以使用平行电流激励。在施加这个激励之后,软件会自动考虑各个导体之间的电磁耦合,计算各个导体上的电流。图5‑6所示为平行电流激励的设置界面,与电流激励相似,但需要注意的是,在施加平行电流激励时,需要同时选择所有并联导体。此外,平行电流激励只适用于2D分析。
5.2.2边界条件
默认边界条件
在模型内部不同实体交界面,默认边界条件为自然边界条件,即在无面电流密度分布的边界,切向H和法向B均连续,即
\[ \begin{array}{l}H_{1 \mathrm{t}}=H_{2 \mathrm{t}} \\ B_{\mathrm{ln}}=B_{2 \mathrm{n}}\end{array} \]
当交界面存在面电流密度分布时,切向H满足以下方程,即
\[ H_{1 \mathrm{t}}=H_{2 \mathrm{t}}+J_{\mathrm{sn}} \]
其中Jsn为与Ht和交界面法向矢量均垂直的方向上的电流密度。具体内容可以查看电磁场边界条件相关书籍。
在求解域的边界,默认边界条件为纽曼边界(Neumann Boundary),即磁场与求解域边界平行。需要注意的是,对于求解域的边界,在3D仿真中可以采用默认边界,而在2D仿真中则必须添加边界条件。
零切向磁场强度(Zero Tangential H Field)
如果已知某个边界的切向磁场强度为零,则可以使用零切向磁场强度边界条件,该边界条件只能用于3D分析中。在磁性材料与空气的交界面,在空气一侧磁力线与交界面垂直。在仿真中,如果关注的是空气中的磁场分布,为了减小仿真模型的尺寸,有时会不对磁性材料建模,这时在交界面处就可以用零切向磁场强度边界条件。
切向磁场强度(Tangential H Field)
如果已知某求解域边界的切向磁场强度,则可以使用切向磁场强度边界条件,该边界条件只能用于3D分析中。图5‑7所示为切向磁场强度设置界面,在U(X)和V(Y)两栏中输入两个正交的磁场强度分量,然后在坐标系选项卡中定义U(X)的方向矢量,V(Y)的方向与U(X)垂直。
零合成切向磁场强度(Integrated Zero Tangential H Field)
如果已知某个边界的切向磁场强度积分为零,则可以使用零合成切向磁场强度边界条件,该边界条件只能用于3D分析中。
绝缘边界(Insulating)
绝缘边界条件主要用于模拟绝缘薄层,只能在3D模型中使用。在有的仿真中,两个导体之间有非常薄的绝缘层,电流无法流通,若直接对该绝缘层进行建模,无疑将增大计算量,这个时候就可以用一个绝缘边界来模拟该绝缘薄层的作用。
对称对边(Symmetry)
对称边界条件与静磁场中的对称边界条件完全相同,在2D和3D仿真中均可使用,这里不再赘述。
主从边界(Master/Slave)
主从边界条件与静磁场中的主从完全相同,在2D和3D仿真中均可使用,这里不再赘述。
阻抗边界(Impedance)
当分析的模型尺寸远大于趋肤深度时,对导体建模并准确的分析其涡流效应需要对导体进行细致的网格划分,这样会极大的增加计算量,导致求解困难,这个时候就可以采用阻抗边界。在使用阻抗边界时,可以不对导体进行建模,具体可以分两种不同的情况。对于如图5‑8所示的情形,被感应导体位于源导体之外,要分析源导体对被感应导体的涡流效应时,可以不对被感应导体建模,只需保证求解域边界与导体内边界重合,然后在边界上施加阻抗边界条件即可。
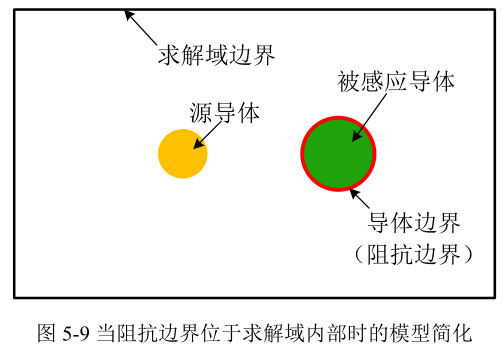
对于如图5‑9所示的情形,被感应导体位于求解域内部,要分析源导体对被感应导体的涡流效应时,需要对被感应导体建模,将其材料设置为完美导体(Perfect Conductor),同时在导体模型中去掉"Solve Inside"勾选(即不计算导体内部的电磁场情况),然后在导体边界施加阻抗边界条件即可。
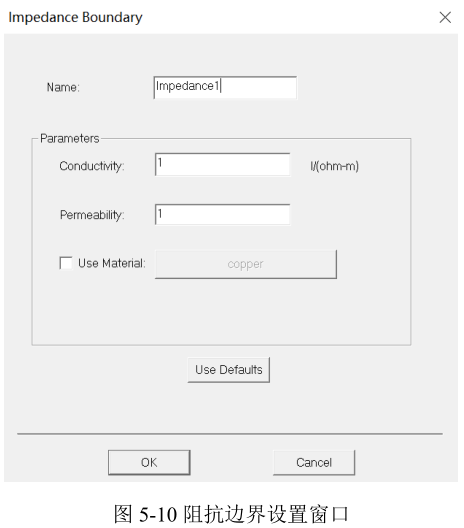
阻抗边界在2D和3D分析中均能使用,图5‑10所示为阻抗边界设置窗口,当采用阻抗边界条件时,只需在设置窗口输入被感应导体材料的电导率和相对磁导率,也可以直接选择导体材料(包括非线性材料)。
5.2.3趋肤效应及趋肤网格划分
涡流效应是由电磁感应产生的,由楞次定律可以知道,感应电流可以阻碍磁场的变化,因而只允许外部磁场渗透到导体的一定深度,感应电流也集中于导体表面的一定深度。这个深度可以用趋肤深度来表征,即
\[ d=\sqrt{\frac{2}{\omega \sigma \mu_{0} \mu_{r}}} \]
其中,ω为角频率,σ为导体的电导率,μ0为真空磁导率,μr为相对磁导率。
由于趋肤效应,趋肤深度尺度内存在很大的场梯度,为了准确的分析涡流效应,一般需要对趋肤层进行较密的网格划分,特别是在趋肤深度相较于模型尺寸较小时。Maxwell有基于趋肤深度的网格细化功能,在2D和3D分析中均可使用,选择需要考虑趋肤效应的导体边界(2D仿真中为边,3D仿真中为面),然后右键选择Assign Mesh Operation → On Selection → Skin Depth Layered Based即可,在设置窗口中输入趋肤深度,或者利用材料参数计算均可。
为了提高计算效率,默认情况下Maxwell是不考虑涡流效应的,因此在设置完趋肤网格之后,还需要告诉程序需要对哪些导体考虑涡流效应,比如,绞线式线圈模型(Stranded)就不需要考虑趋肤效应。在仿真图形窗口单击右键,选择Set Eddy Effects,可以弹出涡流效应设置窗口,如图5‑11所示。设置内容包括涡流效应和位移电流效应,涡流效应只需对导体施加,位移电流效应一般只需对介质施加,但是在低频分析中,一般可以忽略,不用考虑位移电流效应。
5.3 主要后处理方法
5.3.1阻抗矩阵及其参数的计算方法
Maxwell时谐场分析的一个重要用途是分析系统阻抗的频谱特性,即不同频率下系统的阻抗。在低频分析中,|σ|>>|jωε|,即传导电流远大于位移电流,因此主要关注的是系统的电感与电阻。需要注意的是,默认情况下Maxwell是不会计算导体的阻抗的,如果需要计算导体阻抗,需要在工程树下右键Parameters → Assign → Matrix进行设置,计算完成后在Solution Data下的Matrix选项卡查看计算结果。下面就Maxwell中阻抗矩阵的定义及其中电阻与电感的计算方法做简单的介绍。
(1)阻抗矩阵的定义
在Maxwell时谐场分析中,可以通过阻抗矩阵建立起多导体那个中交流电压和交流电流的关系。对于如图5‑12所示的双导体回路系统,其电压、电流关系可表示为
\[ \left\{\begin{array}{l}\Delta V_{1}=I_{1}\left(R_{11}+j \omega L_{11}\right)+I_{2}\left(R_{12}+j \omega L_{12}\right) \\ \Delta V_{2}=I_{1}\left(R_{12}+j \omega L_{12}\right)+I_{2}\left(R_{22}+j \omega L_{22}\right)\end{array}\right. \]
上式可以表示为矩阵形式,即
\[ \left[\begin{array}{c}\Delta V_{1} \\ \Delta V_{2}\end{array}\right]=\left[\begin{array}{cc}Z_{11} & Z_{12} \\ Z_{12} & Z_{22}\end{array}\right]\left[\begin{array}{c}I_{1} \\ I_{2}\end{array}\right] \]
其中,Z11=R11+jωL11为回路1的自阻抗,Z22=R22+jωL22为回路2的自阻抗,Z12=R12+jωL12为回路1与回路2之间的互阻抗。以上阻抗矩阵给出了双回路系统的电压、电流的关系。对于有n个回路的系统,其电压、电流关系可以用n×n阻抗矩阵来描述。以上互感比较容易理解,互电阻R12可以理解为由导体2的电磁感应在导体1上引起的附加损耗。

(2)电感与电阻的计算
在Maxwell中,阻抗矩阵分为电感和电阻两部分计算。计算电感时,求解器首先利用计算得到的磁场计算系统的平均磁能
\[ W_{A V}=\frac{1}{4} \int_{V} \boldsymbol{B} \cdot \boldsymbol{H}^{*} d V \]
其中,上标*表示取复数的共轭。由于系统的瞬时磁能可以表示为
\[ W_{\text {Inst}}=\frac{1}{2} L i(t)^{2} \]
其中,i(t)=Ipeakcos(ωt+θ),Ipeak为电流峰值。平均磁能WAV可以对WInst在一个周期内求平均得到,即
\[ \begin{aligned} W_{A V} &=\frac{1}{2 \pi} \int_{0}^{2 \pi} W_{I n s t} d \omega t \\ &=\frac{L}{4 \pi} \int_{0}^{2 \pi} I_{p e a k}^{2}[\cos (\omega t+\theta)]^{2} d \omega t \\ &=\frac{L}{4} I_{p e a k}^{2} \end{aligned} \]
由此可得,系统电感可以由系统平均磁能和电流峰值得到,即
\[ L=\frac{4 W_{A V}}{I_{p e a k}^{2}} \]
Maxwell中的电阻是通过计算欧姆损耗得到的,首先根据计算得到的电流密度计算导体的欧姆损耗,即
\[ P=\frac{1}{2 \sigma} \int_{V} \boldsymbol{J} \cdot \boldsymbol{J}^{*} d V \]
对于正弦电流而言,欧姆损耗与峰值电流的关系可以表示为
\[ P=R I_{R M S}^{2}=\frac{1}{2} R I_{\text {peak}}^{2} \]
由此,电阻可由欧姆损耗和电流峰值得到,即
\[ R=\frac{2 P}{I_{p e a k}^{2}} \]
5.3.2电磁力和电磁力矩的计算
在Maxwell中,电磁力的计算分为两种,其一是洛伦兹力(Lorentz Force),其二是虚位移力(Virtual Force)。电磁力矩也可以分为这两种。需要注意的是,默认情况下Maxwell是不会计算电磁力和电磁力矩,如果需要计算,需要在工程树下右键Parameters → Assign → Force/Torque进行设置,计算完成后在Solution Data下的Force/Torque选项卡查看计算结果。
(1)洛伦兹力
在Maxwell时谐场中,洛伦兹力表示载流导体在时变磁场作用下产生的平均电磁力。在时变磁场作用下,载流导体受到的瞬时电磁力可表示为
\[ \boldsymbol{F}(t)=\int_{V} \boldsymbol{J}(t) \times \boldsymbol{B}(t) d V \]
其中,J(t)为电流密度,B(t)为磁感应密度。对瞬时电磁力在一个周期内求平均,即可得到载流导体所受洛伦兹力(即平均力),即
\[ \begin{aligned} \boldsymbol{F}_{A V} &=\frac{1}{2 \pi} \int_{0}^{2 \pi} \boldsymbol{F}(t) d \omega t \\ &=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left[\int_{V} \boldsymbol{J}(t) \times \boldsymbol{B}(t) d V\right] d \omega t \end{aligned} \]
洛伦兹力矩表示载流导体在时变磁场作用下产生的平均电磁力矩。在时变磁场作用下,载流导体受到的瞬时电磁力矩可表示为
\[ T(t)=\int_{V} \boldsymbol{r} \times[\boldsymbol{J}(t) \times \boldsymbol{B}(t)] d V \]
其中,r为作用点到旋转轴的位移矢量。对瞬时电磁力矩在一个周期内求平均,即可得到载流导体所受电磁力矩(即平均力),即
\[ \begin{aligned} \boldsymbol{T}_{A V} &=\frac{1}{2 \pi} \int_{0}^{2 \pi} \boldsymbol{T}(t) d \omega t \\ &=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left[\int_{V} \boldsymbol{r} \times[\boldsymbol{J}(t) \times \boldsymbol{B}(t)] d V\right] d \omega t \end{aligned} \]
(2)虚位移力
在Maxwell中,当材料的相对磁导率大于1时,通过计算洛伦兹力和洛伦兹力矩不能得到准确的结果,这是因为,洛伦兹力计算的是传导电流在磁场作用下的受力,而相对磁导率大于1的材料中磁化效应对力的贡献是不能反映在洛伦兹力中的。这个时候,可以采用虚位移力来进行计算。
虚位移力的计算原理是这样的:假设被分析物体存在一个很小的位移ds,计算系统能量的变化dW,这个能量的变化就可以认为是力对物理的做功,则这个力就可以表为dW/ds。由此,在时谐场中,虚位移力计算的也是一个周期内的平均力,即
\[ \boldsymbol{F}_{A V}=\frac{1}{2 \pi} \int_{0}^{2 \pi} \boldsymbol{F}(t) d \omega t=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left[\frac{d W(s, i)}{d s}\right] d \omega t \]
类似的,虚位移力矩可以通过假设一个很小的旋转角再计算系统能量变化得到,即
\[ \boldsymbol{T}_{A V}=\frac{1}{2 \pi} \int_{0}^{2 \pi} \boldsymbol{T}(t) d \omega t=\frac{1}{2 \pi} \int_{0}^{2 \pi}\left[\frac{d W(\theta, i)}{d \theta}\right] d \omega t \]
(3)平均力与瞬时力
由上述可知,Maxwell时谐场给出的力均为平均力,是取的瞬时力在一个周期内的平均,下面我们介绍一下时谐场中瞬时力和平均力的区别。假设电流的函数为I(t)=Imsin(ωt),其产生的磁场与电流同频率,但存在一定的相位差θ,即B(t)=Bmsin(ωt+θ),则
\[ \begin{aligned} F(t) & \propto I(t) \cdot B(t) \\ &=I_{m} \sin (\omega t) \cdot B_{m} \sin (\omega t+\theta) \\ &=\frac{I_{m} B_{m}}{2}[\cos (\theta)-\cos (2 \omega t+\theta)] \end{aligned} \]
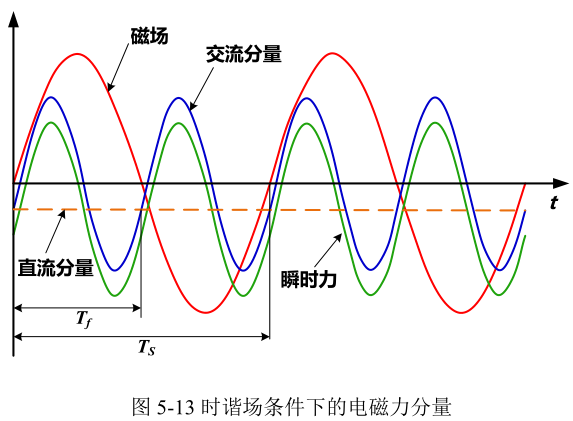
由可知,在时谐场条件下,电磁力瞬时曲线F(t)包含两个分量,一个直流分量和一个交流分量,且交流分量的频率为电流(或磁场)频率的两倍(如图5‑13所示),即
\[ f_{F}=\frac{1}{T_{F}}=2 f_{S} \]
其中,fF为电磁力交流分量频率,TF为电磁力交流分量周期,fS为电流(或磁场)的频率。
5.3.3能量及损耗的计算
(1)磁能的计算
在时谐场中,能量密度包含磁场能和电场能,总能量可以表示为
\[ w=\frac{1}{4} \operatorname{Re}\left[\boldsymbol{B} \cdot \boldsymbol{H}^{*}-\left(\boldsymbol{E} \cdot \boldsymbol{D}^{*}\right)\right] \]
其中,Re表示取复数的实部,上标*表示复数的共轭,符号·表示点乘。在Maxwell的后处理器中,内置有上述能量密度表达式,标记为Energy。对于系统的总能量而言,只需对上式在一定的空间内积分即可,即
\[ W=\frac{1}{4} \int_{V} \operatorname{Re}\left[\boldsymbol{B} \cdot \boldsymbol{H}^{*}-\left(\boldsymbol{E} \cdot \boldsymbol{D}^{*}\right)\right] d V \]
对于低频电磁场问题,|B·H*|>>|E·D*|,即上式计算得到的即为总磁能。如果需要准确的计算系统磁能,可以在场计算器中编写磁能计算表达式进行计算。
(2)磁滞损耗
对于磁性材料内产生的磁滞损耗,其磁滞损耗密度为
\[ p_{h}=\frac{1}{2} \omega \operatorname{Im}\left(\boldsymbol{B} \cdot \boldsymbol{H}^{*}\right) \]
其中,Im表示取复数的虚部,ω表示场量的角频率。在Maxwell的后处理其中,内置的磁滞损耗密度表达式标记为Hysteresis Loss。若要计算某磁性材料的磁滞损耗,只需对上式在一定空间内积分即可,即
\[ P_{h}=-\frac{\omega}{2} \int_{V} \operatorname{Im}\left(\boldsymbol{B} \cdot \boldsymbol{H}^{*}\right) d V \]
(3)欧姆损耗
对于导体中产生的欧姆损耗,其功率密度可以表示为
\[ p_{\mathrm{ohm}}=\frac{J \cdot J^{*}}{2 \sigma} \]
其中,J为电流密度,σ为电导率。在Maxwell的后处理其中,内置的欧姆损耗功率密度表达式标记为Ohmic Loss。如要计算某导体内的欧姆损耗,只需对上式在一定空间内积分即可(涡流损耗就可以通过这个表达式计算),即
\[ P_{\mathrm{ohm}}=\int_{V} \frac{J \cdot J^{*}}{2 \sigma} d V \]
对于阻抗边界,欧姆损耗可以表示为
\[ P_{\mathrm{obm}}=\sqrt{\frac{\omega \mu_{0} \mu_{r}}{8 \sigma}} \int_{S} \boldsymbol{H}_{t} \cdot \boldsymbol{H}_{t}^{*} d S \]
其中,μ0为真空磁导率,μr为相对磁导率,Ht为阻抗边界磁场强度H的切向分量。
5.3.4感应电流的计算
感应电流的计算相对比较简单,只需要导体截面上的法向电流密度积分即可得到,即
\[ I=\int_{S} \boldsymbol{J} \cdot d \boldsymbol{S} \]
在利用场计算器进行计算时,需要分别对电流密度的实部和虚部进行积分计算,具体内容参见后文中的案例。上述内容介绍了一些后处理相关计算的原理及对应的表达式,在Maxwell场计算器中如何实现,请参考文献[2]和后文中的相关案例。
5.4 案例1------三相电缆的阻抗分析
电缆在电力行业中有着广泛的应用,是电力传输的主要设备之一,主要包含金属导线和绝缘两部分。某型号三相电缆如图1(a)所示,其金属导线材料为铜(红色),外层包裹绝缘层(蓝色),内绝缘层内径为R1=10mm,外径为R2=15mm,外绝缘层(黑色)的厚度为W=5mm,如图1(b)所示。假设内、外绝缘层及其间的填充物相对介电常数为10。由于系统中的非线性设备的存在,电网中往往存在着大量的谐波,不同的谐波频率下,电缆将呈现出不同的阻抗,现分析该电缆的阻抗特性(频率范围在10kHz以内)。
5.4.1本节知识点
基于趋肤深度的网格划分
趋肤效应和邻近效应
基于场计算器的交流电阻的计算
交流阻抗与频率的关系
动画显示
5.4.2分析模型的建立
(1)确定分析类型
对于电力电缆而言,其工作频率为工频(50Hz),由此可以确定该分析的类型是涡流场(Eddy Current)。此外,由于电缆长度一般远大于其截面尺寸,属于长直模型,因此可采用2D平面(Cartesian,XY)模型进行简化。
点击Insert Maxwell 2D Design图标,新建一个2D仿真任务,然后点击工具栏Maxwell 2D → Solution Type,弹出新的对话框中,在Geometry Mode选择Cartesian, XY,求解器选择Eddy Current。
(2)建立分析模型
涡流场分析对应的方程为
\[ \nabla \times\left(\frac{1}{\mu_{r} \mu_{0}} \nabla \times \boldsymbol{A}\right)=(\sigma+j \omega \varepsilon)(-j \omega \boldsymbol{A}-\nabla \phi) \]
其中,σ为导体电导率,表征的是导体内的传导电流,ε为介质介电常数,在这里ωε表征的是由介质极化产生的位移电流。一般而言,σ>>ωε,因此分析中可以忽略由介质极化产生的位移电流。另外一方面,由于绝缘介质的相对磁导率与空气相当,因此可直接将其视为空气,只对导体进行建模,这样就极大的简化了分析模型,可以提高计算效率。
基于上述分析,建模过程如下:
为了方便建模,可事先定义相关模型参数。右键点击模型树中新建的任务Maxwell2DDesign1 (EddyCurrent, XY),选择Design Properties,在新弹出的对话框中,点击左下角的Add...,在Name栏输入R1,在Unit Type栏选择Length,在Value一栏输入10,即定义内绝缘层内径为R1,值为10mm。
采用类似的方法定义内绝缘层的外径为R2=15mm,导体圆心对应半径R3=2/sqrt(3)*R2。
首先建立第一个导体的模型。点击绘图工具栏中的Draw circle,在绘图窗口创建一个圆,然后点击模型工作树下的Sheets → vacuum → Circle1 → CreateCircle,在Center Position处输入(R3,0,0),在Radius处输入R1。在Maxwell的建模对话框中,即建模时右下角的数据输入框中不能输入变量,因此需先完成建模再在CreateCircle对话框中修改参数,实现参数化建模。
由于三个导体在空间位置上具有一定的特点,另外两个导体可以采用复制的方法进行建模。右键点击Circle1,选择Edit → Duplicate → Around Axis,在Axis中选择Z,Angle中输入120,Total number中输入3,然后分别将三个圆重新命名为PhaseA,PhaseB和PhaseC。
最后建立求解域的模型。点击绘图工具栏中的Create region,选择Pad all directions similarly,即所有方向设置参数一样,在Percentage Offset中输入300,即求解域尺寸定义为模型尺寸的3倍。最终得到的分析模型如下图所示。
(3)设置材料属性
根据上述分析,绝缘材料可以直接当空气处理,因此材料设置中只需要设置两种材料。将导线材料设置为铜(copper),求解域采用默认的真空。
(4)基于趋肤深度的网格剖分
对于导线,在高频下会有明显的趋肤效应,电流会集中在导线的表面,因此需要对导线表面的网格进行比较细致的划分,得到比较合理的初始网格,减少跌到次数,提高计算精度和效率。可以根据式事先预估分析频率下的导体趋肤深度,如果趋肤深度较导体尺寸小很多,则需要对导体进行基于趋肤深度的网格划分;反之,则采用常规网格划分即可。
首先,选择所有导线的边线,右键选择Assign Mesh Operations → On Selection → Skin Depth Layered Based,即根据趋肤深度来设置网格划分的尺寸,其中的On Selection可以理解为在边界周围进行网格细化。然后点击Calculate Skin Depth,在频率出输入1kHz,软件会自动计算该频率下的趋肤深度(2.09mm),设置边界上的网格层数(Number of Layers)为4。注意,网格层数有2~4层即可,层数过多会导致计算量太大,降低计算效率。
对于求解域而言,网格相对简单,选择region,右键选择Assign Mesh Operations → In Selection → Length Based,其中的In Selection可理解为在模型内部进行划分。在最大网格尺寸(Maximum Length of Elements)处输入10mm即可。
5.4.3单导体的阻抗特性分析(趋肤效应)
(1)施加载荷和边界条件
本案例中的导线是线性材料,其阻抗与电流大小没有关系,分析中可以将其电流设置为1A。这里首先考虑单根导体的阻抗分析,即只在PhaseA导体上施加电流,选择PhaseA导体,单击右键,点击Assign Excitation → Current,在Name栏中输入Ia,在Value栏输入1A,其他采用默认值。
对于边界条件而言,在所有外边界施加气球边界(Balloon)模拟无穷远边界即可。
(2)求解设置与求解
在工程树Analysis中右键选择Add Solution Setup,在General中将Percent Error设置为0.01;在Solver中将Adaptive Frequency设置为1kHz。
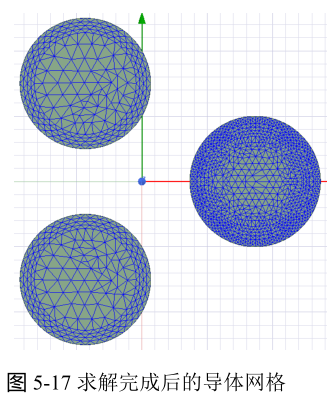
设置完成后,右键工程树下的Setup1,选择Apply Mesh Operations,进行初始网格剖分。选择导线模型,右键选择Plot Mesh,可以看到导体的初始网格如下,网格在导体表面加密,中心则相对稀疏。
点击Validate检查模型,会出现警告信息"Eddy effect settings...",即提醒你没有设置需要对哪些导体进行涡流效应的分析,默认条件下软件不会考虑涡流效应。在很多分析中,我们并不需要考虑所有导体的涡流效应,比如在对变压器绕组建模时我们一般将其等效为单个导体,而实际中它是多匝导线密绕而成的(绞线导体,Stranded类型),电流在整个模型的截面上是均匀分布的。又比如,在较为复杂的分析模型中,需要考虑涡流效应的导体也有主次之分,对所有导体都考虑趋肤效应会增加额外的计算量,这个时候就需要告诉软件需要考虑哪些导体的涡流效应。在本次分析中,我们只考虑单导体的涡流效应,因此只对PhaseA导体进行涡流效应设置。单击右键,选择Assign Excitation → Set Eddy Effects,只勾选PhaseA导体。
最后,点击Analyze All,对仿真模型进行求解。
待模型求解完成,三个导体的网格如下图所示,只有PhaseA导体的网格被加密。这是因为,分析中另外两个导体没有施加电流载荷,也没有考虑涡流效应,这两个导体在这里与空气无异,没有很明显的场的梯度,在迭代过程中没有进行特别的加密。
(3)查看电流密度分布
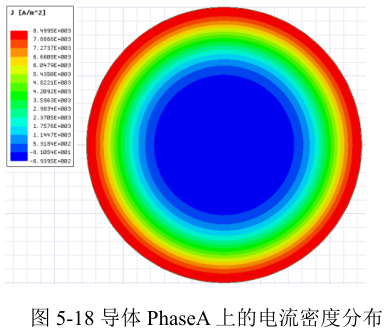
计算完成之后,删除Field Overlays下面的MeshPlots,选择导线PhaseA,右键选择Fields → J → JAtPhase,图形窗口会显示导线上的电流密度分布,如下图所示。由计算结果可知,导线电流基本集中于表面,即表现出明显的趋肤效应。
(4)计算导线的阻抗
在直流情况下,电流均匀分布在导体截面上,导体的有效载流面积为其整个截面;而在交流情况下,特别是高频情况下,电流趋于表面分布,导体的有效载流面积减小,电阻会增加。对于我们分析中的情形,r=10mm,则可计算出PhaseA导线单位长度的直流电阻为
\[ R_{D C}=\frac{1}{\pi \sigma r^{2}}=54.9 \mu \Omega / \mathrm{m} \]
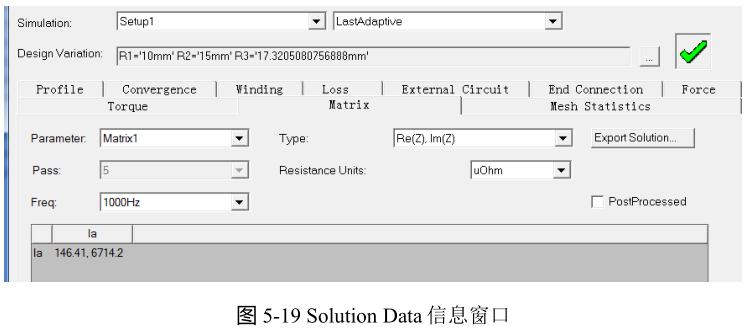
基于Maxwell计算导体的交流电阻。在Maxwell中计算PhaseA导线的阻抗,右键点击工程树下的Parameters,选择Assign → Matrix,勾选Ia,点击确认后再次点击Analyze All,计算完成后点击Solution Data,如下图所示。其中Z为计算出来的阻抗,Re(Z)为阻抗的实部,即导线的电阻,Im(Z)为阻抗的虚部,即导线的感抗(jωL),即Z=R+jωL。计算得到的电阻为146.4μΩ,为直流电阻的2.7倍,感抗为6.71mΩ,对应的电感为1.07uH。
在静磁场分析中,我们学习过通过能量法计算线圈的电感,在涡流场中同样也可以通过能量法计算电感,这里不再赘述。对于电阻的计算,我们可以采用类似的方法,即通过计算导体的欧姆损耗来计算电阻,即
\[ \frac{1}{2} I^{2} R=P \Rightarrow R=2 P / I^{2} \]
需要注意的是,在Maxwell的涡流场分析中,所有的场量均用峰值表示,所以上述表达式中乘上了一个1/2。
损耗的计算方法有两种,其一是用Maxwell自带的欧姆损失功率密度函数,具体过程如下:右键单击Field Overlays → Calculator;点击Input → Quantity,选择Ohmic-Loss(内置的式);点击Input → Geometry,选择Volume → PhaseA;点击Scalar → 积分(ʃ);点击Output → Eval,计算得到的欧姆热功率为73.2μW,利用上式即可计算得到导体电阻为146.4μΩ,与基于Matrix计算得到的结果相同。
第二种方法是基于欧姆损耗的物理定义,即
\[ P=\int_{V} \rho J^{2} d V \]
具体过程如下:点击Input → Quantity,选择J;点击Vector → Scal?,选择ScalarZ(2D平面坐标系中电流只有Z分量,这里是将电流矢量取为标量);点击General → Complex,选择CmplxMag(涡流场中场量均以复数表示,电流密度平方之前需取模值,或者用J·J*的形式进行计算也可以);点击Input → Number,选择Scalar,在Value处输入2;点击Scalar → Pow;点击Input → Number,选择Scalar,在Value处输入58e6(铜的电导率);点击General →除(/);点击Input → Number,选择Scalar,在Value处输入2;点击General →除(/);点击Input → Geometry,选择Volume → PhaseA;点击Scalar → 积分(ʃ);点击Output → Eval,计算得到的欧姆热功率为73.2μW。需要注意的是,Maxwell涡流场分析中,所有的场量都以复数表示,因此在求平方之前需要取其模(CmplxMag),或者采用共轭复数相乘的方式。此外,Maxwell涡流场分析中所有的场量均以峰值表示,因此在取平方后还需要除2。
上述两种方法计算欧姆损耗的表达式如下图所示。
(5)不同频率下的阻抗分析
以上分析的是单频点的导线阻抗,Maxwell还提供了扫频功能,可以同时计算多个频点下的涡流场。操作如下:双击工程树下的Analysis → Setup1,点击Frequency Sweep,在Start处输入1kHz,在Stop处输入10kHz,在Step处输入1kHz,即分析频率范围为1kHz~10kHz,每1kHz一个计算点。然后点击Analyze All。
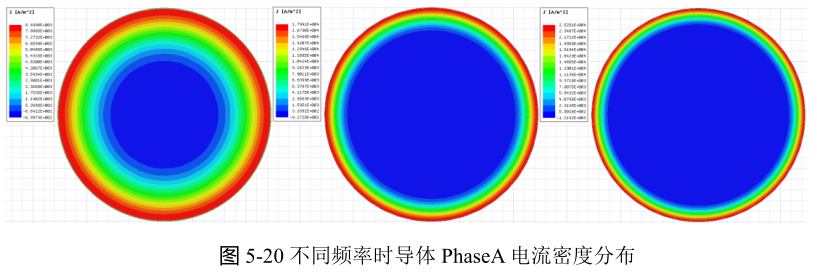
等计算结束,分别绘制不同频率(1kHz、5kHz和10kHz)下的导体表面电流分布,如下图所示,频率越高,趋肤效应越明显。
Maxwell还提供了然后生成不同频率下的导线阻抗曲线。右键点击工程树下的Results,选择Create EddyCurrent Report → Rectangular Plot,在Category中选择L,点击New Report;在Category中选择R,点击Add Trace。计算得到的结果如下图所示,随着频率的升高,导线电阻明显增加,但电感略微减小。
电阻的增加很好理解,因为频率越高,趋肤效应越明显,当导线半径远大于趋肤深度时,即r>>d时,导体的有效载流截面可表示为s=2πrd,即。对于电感的变化,可以从磁能的角度来解释。对于单根导线而言,其总的载流量恒定,由B=μ0I/2πr可知,导体外的磁场分布保持不变,即导体外的磁能保持不变;但是对于导体内部而言,由于趋肤效应的影响,电流趋肤到导线表面,导线内部磁场减弱,磁能减小。一般而言,导线内部磁能只占导线电流产生总磁能的极少一部分,因此电感的变化也不明显。关于导线的内自感和外自感的计算方法有兴趣的同学可以参考电磁场相关书籍。
为验证上述分析,可绘制不同频率下导体内部和外部的磁能曲线。具体操作如下:右键单击Field Overlays → Calculator;点击Input → Quantity,选择Energy(内置的式);点击Input → Geometry,选择Volume → PhaseA;点击Scalar → 积分(ʃ);点击Add,在Name出输入Ein,即将导体内的磁能表达式定义为Ein。点击Input → Quantity,选择Energy;点击Input → Geometry,选择Volume → AllObjects;点击Scalar → 积分(ʃ);点击Add,在Name出输入Eall,即将导空间总磁能表达式定义为Eall。
右键点击工程树下的Results,选择Create Fields Report → Rectangular Plot,在Category中选择Calculator Expression,Quantity中选择Ein,点击New Report;在Category中选择Calculator Expression,在Y中键入Eall-Ein(即导体外磁能),点击New Report,如图5‑22所示。由计算结果可知,不同频率下,导体外磁能基本保持不变,而内部磁能则变化较为明显。另外一方面,对比导体内部磁能和总磁能可知,导体内部磁能占总磁能的比例不到4%,因而对导线电感的变化影响很小。
5.4.4三相导线的阻抗分析(邻近效应)
(1)求解设置
现在同时考虑三个导线的涡流效应。右键单击右键,选择Assign Excitation → Set Eddy Effects,同时勾选PhaseA、PhaseB和PhaseC三个导体。同时,在另外两个导体上施加电流载荷:选择PhaseB导体,单击右键,点击Assign Excitation → Current,在Name栏中输入Ib,在Value栏输入1A,Phase栏输入-120,其他采用默认值。PhaseC导体的设置类似,不同之处在于需将其相位设置为120。设置完成后点击工程树下的Parameters → Matrix,同时勾选三个导体。然后右键点击工程树下的Analysis → Setup1,选择Revert to Initial Mesh,清空之前的计算数据与网格,然后再以类似的操作选择Apply Mesh Operations,重新添加网格,最后Analyze All。
计算完成后,选中三个导体,单击右键,选择Plot Mesh,得到三个导体的网格如下图所示,三个导体的网格均被加密,这是因为三个导体都考虑了涡流效应。
(2)查看电流密度
删除Field Overlays下面的MeshPlots,选择导线PhaseA、PhaseB和PhaseC三个导体,右键选择Fields → J → JAtPhase,图形窗口会显示导线上的电流密度分布,如下图所示。点击工程树下的Field Overlays → J → JAPhase,在Properties信息栏里可以修改该电流密度云图的相位信息,下图分别为相位为0o、120o和240o时的电流密度分布云图。
对比仅考虑单根导线时的电流分布,此时导线上的电流分布不再具有沿圆周的对称性,三相导体电流呈现出相互吸引的特点,即电流更趋向分布于两导体相互临近的部分,这就是所谓的"临近效应",即相互靠近的两根导体相互影响。
(3)绘制电流密度矢量图
选中三个导体,单击右键,选择Fields → J → J_Vector,同时对模型进行旋转,即可显示三根导体电流密度的矢量图,如下图所示。
Maxwell还有生成动画的功能。点击工程树下的Field Overlays,单击右键,选择Animate,在Start栏输入0,在Stop栏输入350,在Step栏输入10,即生成36帧动画,每10o一帧,点击OK按钮即可生成动画。
(4)计算导线的阻抗
点击Solution Data,在Matrix一栏可以看到计算得到的三个电流之间的阻抗矩阵,如下图所示,在Type栏可以修改阻抗显示的形式。
其中Matrix(Ia, Ia) = (196.36μΩ, 1.0346uH)为导体A的自电阻和自电感,Matrix(Ia, Ib) = (3.3667μΩ, 0.82207uH)为导体PhaseA和导体PhaseB之间的乎电阻和互电感,互电阻的概念可以理解为电流Ib在导体PhaseA上引入的额外损耗对应的电阻。
5.5 案例2------电磁炉感应加热
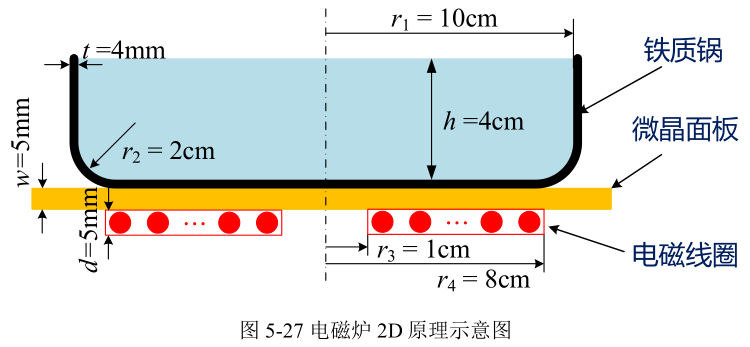
电磁炉是非常常见的家用电器,其基本原理就是电磁感应。图5‑27所示为电磁炉的原理示意图,最底下为交流通电线圈,其上部为微晶面板,主要其绝缘及支撑金属锅的作用。当金属锅放在微晶面板后,底部交流通电线圈产生的交变磁场会在金属锅内产生感应电流,进而产生焦耳热,最终达到加热食物的目的。
假设线圈总计N=14匝,每匝工作电流为I=20A,工作频率为f=1kHz,微晶面板的材料为玻璃,铁质锅的电导率为σ=1e6S/m,相对磁导率为μr=1000,计算该电磁炉上感应出的电流大小及其加热功率。实际的铁质锅的尺寸与厚度差异较大(直径/厚度>100),且工作频率一般在20kHz以上(人耳可闻声波频率以上),图5‑27中的模型参数和上述工作参数都做了相应的简化处理,以减小计算量。
一般而言,电磁炉所用的锅必须是铁锅,因为其磁导率更大,可以增大涡流,从而增大加热功率。另外还有一种说法是,铁锅可以起到屏蔽磁场的作用,减少磁场的辐射,对人体而言更加安全。请将图5‑27中的铁质锅换成相同形状的铝制锅,加以对比分析,验证上述两个结论。
5.5.1本节知识点
二维轴对称建模
感应电流的计算(场计算器)
感应加热功率计算
特定直线上的计算结果提取
5.5.2分析模型的建立
(1)确定分析类型
由计算条件可知,要分析特定频率下电磁炉的涡流发热,明显是时谐场问题。由于铁质锅和电磁线圈一般都是圆形,在图5‑27也采用的圆柱坐标表示,因此可采用2D轴对称分析。
点击Insert Maxwell 2D Design图标,新建一个2D仿真任务,然后点击工具栏Maxwell 2D → Solution Type,弹出新的对话框中,在Geometry Mode选择Cylindrical about Z,求解器选择Eddy Current。
(2)建立分析模型
由于分析的频率较低,可以忽略介质的极化效应,因此,分析中可以不用对微晶面板进行建模,只需要考虑电磁闲钱和铁质锅。此外,由于电磁线圈由多匝密绕而成,每匝电流相同,为简化分析,可将电磁线圈的多匝导体等效为一个整体。所建立的分析模型图5‑28所示,在画铁质锅的圆角时,可以先画出一整个圆环,然后再用Edit → Boolean→ Split进行分割,得到1/4圆环。具体建模过程请参考文献[1]。分别将铁质锅和电磁线圈模型命名为Coil和Pot。
(3)设置材料属性
对于电磁线圈而言,由于为密绕线圈,不需要计算电流分布,且单匝线圈电流已知,其材料不影响计算结果,随意设置一种导体即可,大多数线圈均由铜线绕制,这里将其设置为铜导体(copper)。对于铁质锅,根据分析输入,需要设置其电导率和相对磁导率,在模型树下选择铁质锅模型,单击右键选择Assign Material,弹出材料设置对话框后选择Add Material,在相对磁导率栏填入1000,在电导率栏填入1e6即可,其他均采用默认值。求解域采用默认的真空。
(4)基于趋肤深度的网格剖分
由分析模型可知,铁质锅靠近线圈一侧将存在趋肤效应,因此需要对该边附近的区域进行基于趋肤深度的网格剖分。首先,选择铁质锅上最靠近电磁线圈的直线边和弧线边,右键选择Assign Mesh Operations → On Selection → Skin Depth Layered Based,然后点击Calculate Skin Depth,在频率出输入1kHz,软件会自动计算该频率下的趋肤深度(0.5mm),设置边界上的网格层数(Number of Layers)为2。此外,选择整个铁质锅,右键选择Assign Mesh Operations → Inside Selection → Length Based,输入最大网格尺寸1mm。对于电磁线圈,设置最大网格尺寸3mm,求解域设置为10mm。
5.5.3铁质锅的涡流分析
(1)施加载荷和边界条件
本案例中,只需电磁线圈上设置电流激励即可,线圈总计14匝,每匝电流20A,即总计施加280A的电流,线圈建模为一个整体后,即相当于是绞合导线,类型设置为Stranded即可。
对于边界条件而言,对称轴上采用奇对称边界条件(Flux Tangential),在其他外边界施加气球边界(Balloon)模拟无穷远边界即可。
(2)求解设置与求解
在工程树Analysis中右键选择Add Solution Setup,在General中将Percent Error设置为0.01;在Solver中将Adaptive Frequency设置为1kHz。
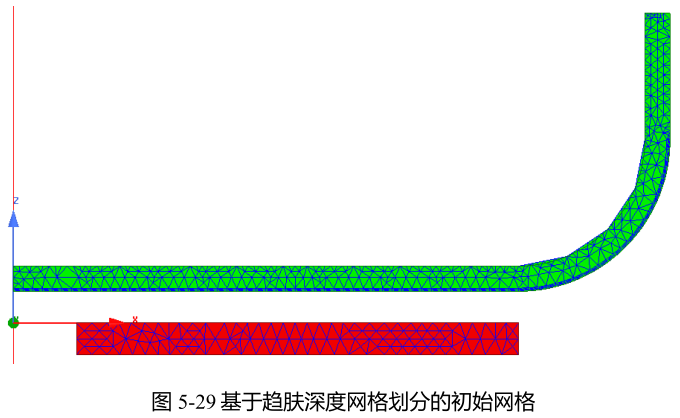
设置完成后,右键工程树下的Setup1,选择Apply Mesh Operations,进行初始网格剖分。选择电磁线圈和铁质锅模型,右键选择Plot Mesh,可以看到导体的初始网格如下,铁质锅靠近电磁线圈一侧的网格有加密。
然后设置涡流效应。单击右键,选择Assign Excitation → Set Eddy Effects,由于电磁线圈是密绕的,电流已知,我们也并不关心其电流的具体分布,因此只需勾选铁质锅模型,即只对铁质锅考虑涡流效应。
最后,点击Analyze All,对仿真模型进行求解。
待模型求解完成,电磁线圈与铁质锅的网格如下图所示,铁质锅靠近电磁线圈一侧被明显加密,而电磁线圈却没有怎么被加密。由于趋肤效应,铁质锅内的场梯度很大,而电磁线圈由于未考虑趋肤效应,场梯度相对小得多。
(3)查看电流密度分布
计算完成之后,删除Field Overlays下面的MeshPlots,选择铁质锅模型,右键选择Fields → J → JAtPhase,图形窗口会显示铁质锅上的感应电流密度分布,如下图所示。由计算结果可知,感应电流基本集中于靠电磁线圈一侧,且方向与电磁线圈电流方向相反(蓝色部分,为负值)。
(4)感应电流及损耗计算
下面来计算铁质锅上的感应电流及欧姆损耗的大小。首先计算涡流损耗,右键单击工程树下Field Overlays → Calculator;点击Input → Quantity,选择Ohmic-Loss(内置的式);点击Input → Geometry,选择Volume → Pot;点击Scalar → Integral(RZ);点击Output → Eval,计算可得总损耗约为1.2W(因为我们设置的工作频率较低,模型小,电磁线圈整体的激励也较小,所以损耗较低,计算机能力较强的同学可以将工作频率设置得更高一点,如10kHz,重新计算涡流损耗,约28.2W)。
再来计算铁质锅上的感应电流。右键单击工程树下Field Overlays → Calculator;点击Input → Quantity,选择J;点击Vector → Scal?→ ScalarPhi(即取环向电流密度);点击General → Complex → Real,即取电流密度实部;点击Input → Geometry,选择Surface→ Pot;点击Scalar → Integral(XY)(在所选平面内进行电流密度积分);点击Output → Eval,计算可得感应电流实部为-14.7A。采用类似的方法计算感应电流的虚部为-13.0A,即总感应电流为-(14.7+j13.0)A。当频率为10kHz时,感应电流为-(44.1+j30.1)A。需要注意的是,在Maxwell中所有的场量均以复数表示,在进行电流密度的积分时,不能先取模值再积分,只能对其实部和虚部分别积分。
图5‑32所示为电磁线圈电流与感应电流之间的相位关系图,其中粗体表示向量。电磁线圈电流I0相位为零,位于实轴上,其在铁质锅内产生的感应电压可以用二者之间的互感表示,即U=-jωMI0,相位滞后源电流90o,位于虚轴的负半轴。铁质锅内的电流可以用感应电压除以其自身阻抗表示,滞后电压一个小于90o的角度。
有兴趣的同学还可以做一下扫频分析,计算不同频率下铁质锅上的感应涡流及对应的涡流损耗。
(5)辐射场的提取
为了验证铁质锅可以屏蔽磁场,减小磁场辐射的说法,现在我们来分析一下该电磁炉的辐射场大小。为了分析电磁炉产生的磁场分布,我们可以在电磁炉附近画几条线段,然后查看这几条线段上的磁场分布。
点击Draw Line,此时程序会提示"A solution exists; do you want to create a non model object?"即已经存在计算结果,此时创建的模型不能作为仿真模型用。但是non model的线条可用用来提取计算结果,但为了更准确的提取计算结果,最好的做法是这些观察线上预设较密的网格。此时,需要清除已有计算结果,再创建所需的线段。右键单击工程树下的Setup1,选择Revert to Initial Mesh,然后点击Draw Line创建三条线段,最上面一条线段的端点坐标为(120mm, 0, 60mm)和(220mm, 0, 60mm),每条线段的间距为40mm,如图 5‑33所示。
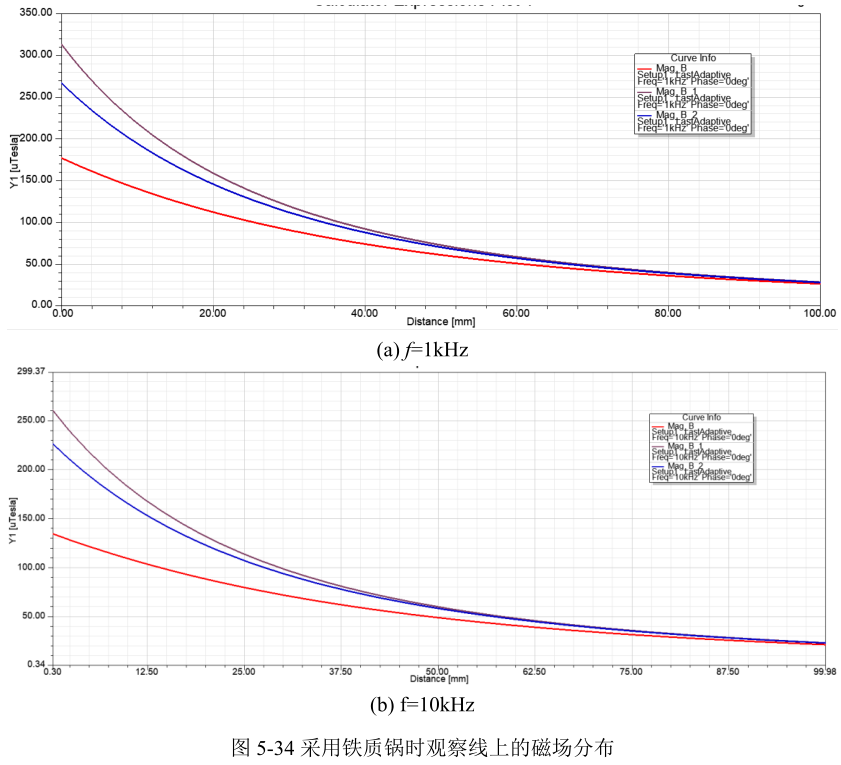
由于需要观察线段上的磁场分布,为了获得较为准确的结果,我们还需要设置这几条观察线的网格,参考之前的设置操作,将观察线的网格设计为5mm。然后右键单击工程树下的Setup1,选择Apply Mesh Operation,然后开始计算。计算完成后,右键单击工程树下的Results,选择Create Fields Report → Rectangular Plot,在左侧的Geometry中选择第一条线段,在主框中的Quantity下选择Mag_B,然后点击下面的New Report,即创建进行报告图。然后选择第二条线段,单击下方的Add Trace,即在之前生成的报告图上增加新的曲线。对于第三条线,采用同样的操作。得到的三条观察线上的磁场分布如下图所示,随着距离的增加,磁场呈现衰减的趋势,频率升高后杂散磁场有所减小,最靠近电磁炉的区域磁场在150uT~300uT之间。
5.5.4铝质锅的涡流分析
将铁质锅的材料换成铝(Aluminum),重复以上分析,与铁质锅的分析结果进行对比,请同学参考上述操作自行完成。
在1kHz时,涡流损耗约为0.75W,感应电流为-(214.0+j12.6)A;在10kHz时,涡流损耗约为2.7W,感应电流为-(216.7+j3.0)A。铝制锅的感应涡流较铁质锅要大得多,且随频率变化不明显,这是因为铝的电导率(3.8e7)较铁要大得多(38倍),其感应电流可表示为
\[ I_{p o t}=\left|\frac{-j \omega M I_{0}}{j \omega L+R}\right| \approx \frac{M}{L} I_{0} \]
即在|jωL|>>R时,感应电流与频率无关,由于铝的电阻率很低,这个条件很容易满足。
此外,还可以关注到,虽然铝制锅的感应电流较铁质锅大得多,但是涡流损耗却小得多,在高频时更加明显,这是因为铁的电阻更高。电磁炉一般工作在20kHz以上,采用铁质锅在增加涡流损耗方面具有优势。
再来看一下对磁场的屏蔽效果。图5‑35所示为采用铝制锅时观察线上的磁场分布,最靠近电磁炉的区域磁场在10uT~60uT之间,较采用铁质锅时小得多。由此可见,题中的第二个说法不准确。这是因为,磁场的屏蔽有两种:第一种是铁磁屏蔽,即利用铁磁材料的导磁特性,将磁力线都限制在铁磁材料中来实现磁场的屏蔽,在静磁场和低频磁场的屏蔽中应用较多;第二种是感应屏蔽,即利用电磁感应产生反向电流,来抵消源磁场,以达到屏蔽的目的,在高频磁场的屏蔽中应用的较多。在上述分析中,铝制锅总感应电流为源电流(电磁线圈电流)的77%,且方向基本相反(相角差179.2o),可以实现很好的感应屏蔽;而铁质锅的总感应电流仅为源电流的19%(10kHz),且与源电流方向并不完全相反(相角差约为146o),感应屏蔽效果有限。
5.6 案例3------三相穿墙交流母线的电磁屏蔽
三相交流母线是电力、工业中常用的设备,用来传输三相电能。三相交流母线一个重要的应用场合是整流系统,用于连接整流变压器和整流器。一般而言,整流变压器安装于室外,整流器安装于室内,三相交流母线需要穿过墙壁,如图5‑36所示。
在大功率应用场合,交流母线的电流可能达数十kA,将在周围产生很强的交变磁场,将引起建筑墙体内钢筋材料的涡流发热,影响其结构稳定性。因而,在大功率应用场合,穿墙母线一般需要配备屏蔽装置,以降低其对建筑钢筋的影响。
图5‑37所示为某型三相穿墙交流母线的二维示意图,三相母线的半径r=20mm,母线之间的间距d=100mm,穿墙孔的宽度为w=320mm,高度h=120mm。问题:(1)假设三相母线电流峰值Ipeak=10kA,计算三相母线在墙壁上产生的磁场分布;(2)假设在窗墙孔上布置铝制屏蔽层,研究屏蔽层屏蔽效果与屏蔽层厚度的关系;(3)计算屏蔽层上的附加损耗与屏蔽层厚度的关系。
5.6.1本节知识点
感应屏蔽的原理
增加屏蔽前后的磁场分布查看与对比
附加损耗的计算
屏蔽效果与屏蔽体厚度的关系
5.6.2分析模型的建立
(1)确定分析类型
由计算条件可知,分析的是三相交流母线的屏蔽问题,属于时谐场问题。由于三相母线的长度相对于其截面尺寸要大得多,因此可以用2D平面模型进行分析。
点击Insert Maxwell 2D Design图标,新建一个2D仿真任务,然后点击工具栏Maxwell 2D → Solution Type,弹出新的对话框中,在Geometry Mode选择Cartesian, XY,求解器选择Eddy Current。
(2)建立分析模型
根据图 5‑37所示的模型和尺寸,建立如图5‑38所示的2D仿真分析模型。建模时,需要对三相母线(红色、黄色、绿色)和屏蔽层(蓝色)单独建模;为了方便观察墙体上的磁场分布,在屏蔽层外创建一个观察区(粉红色);在屏蔽体上方再画一条水平直线,长度与穿墙孔宽度相同,距离为20mm,以方便提取磁场计算数据。此外,建模时,屏蔽层厚度取为10mm,同时将屏蔽层的厚度设置为变量(变量名取为thick),方便后面的参数化扫描分析。具体建模方法请参考文献[1]。建模完成后,将屏蔽层命名为Shielding,将观察区命名为Observation。
(3)设置材料属性
首先分析不考虑屏蔽的磁场分布,此时,只需将三相母线的材料设置为铜(copper),其他的均采用默认材料。
(4)网格剖分
对于铝而言,工频下的趋肤深度约为11mm;对于铜而言,工频下的趋肤深度约为9mm。相较于导体尺寸而言(直径40mm),趋肤深度并不足够小,不需要进行趋肤深度的网格划分。将三相母线及屏蔽层的网格尺寸设置为8mm,将观察区网格设置为20mm,将求解域的网格尺寸设置为40mm。
5.6.3无屏蔽时的磁场分布分析
(1)施加载荷和边界条件
对三相交流母线分别设置电流激励,电流为10kA,导体类型设置为Solid,相位分别为-120o,0和12o。边界条件只需外空气域的边界设置为气球边界(Balloon)以模拟无穷远。
(2)求解设置与求解
在工程树Analysis中右键选择Add Solution Setup,在General中将Percent Error设置为0.01;在Solver中将Adaptive Frequency设置为50Hz。
设置完成后,右键工程树下的Setup1,选择Apply Mesh Operations,进行初始网格剖分。
然后设置涡流效应。单击右键,选择Assign Excitation → Set Eddy Effects,对三相导体设置涡流效应。
最后,点击Analyze All,对仿真模型进行求解。
(3)查看墙体上的磁场分布
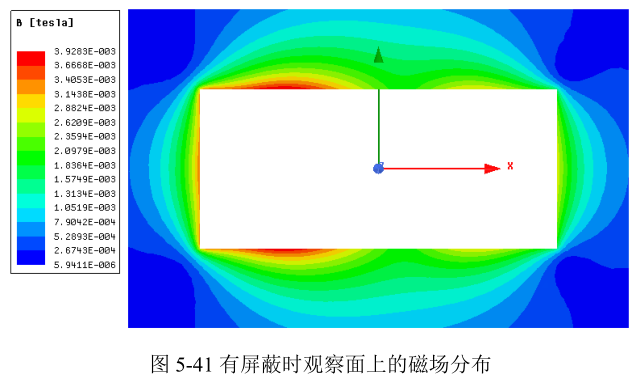
计算完成之后,选择观察区,右键选择Fields → B → Mag_B,图形窗口会显示墙体上的磁场分布,如下图所示。由计算结果可知,墙体上的最大磁场约为15mT。
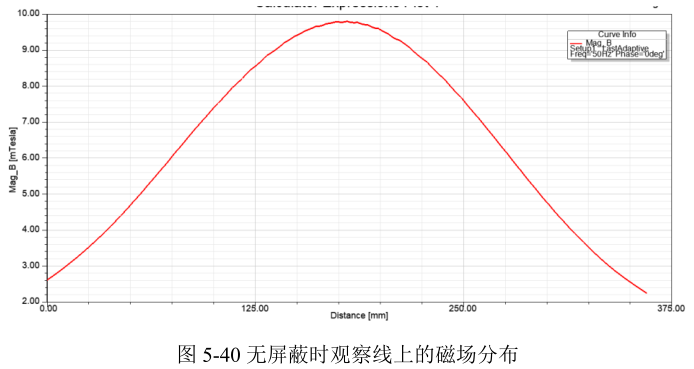
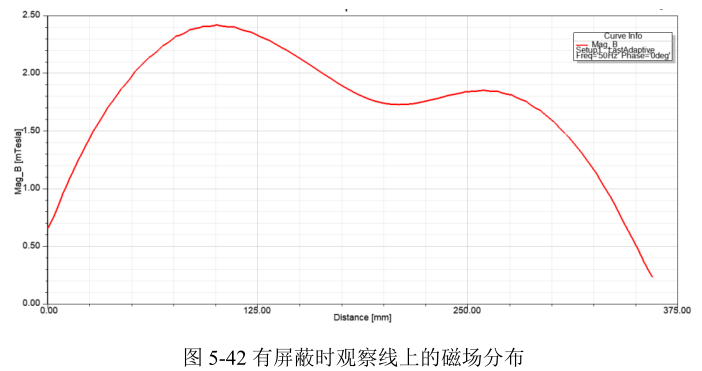
进一步查看观察线上的磁场分布。右键单击工程树下的Results,选择Create Fields Report → Rectangular Plot,在左侧的Geometry中选择观察线,在主框中的Quantity下选择Mag_B,然后点击下面的New Report,即创建进行报告图,如下图所示。由下图可知,观察线上的峰值磁场约为10mT左右。
5.6.4考虑屏蔽时的磁场分布分析
(1)thick=10mm时的屏蔽分析
将屏蔽层的材料换成铝(Aluminum),重复以上分析,与无屏蔽时的分析结果进行对比,请同学参考上述操作自行完成。
计算结果如图 5‑41和图5‑42所示,观察面上的最大磁场为3.9mT,观察线上的最大磁场强度为2.4mT,较无屏蔽时降低了很多。
(2)不同屏蔽层厚度下的屏蔽效能
接下来分析不同屏蔽层厚度下的屏蔽效能,首先定义屏蔽效能为
\[ d B=-20 \lg \frac{\max (B)}{B_{\max }} \]
其中,max(B)表示不同屏蔽层厚度下计算得到的观察区的最大磁场,Bmax=15mT为无屏蔽时观察区上的最大磁场。
然后利用场计算器定义上述屏蔽效能,具体操作如下:右键单击工程树下的Field Overlays → Calculator:点击Input → Quantity → B;点击Vector → Mag (取磁场的模值);点击Input → Geometry → Volume → Observation;点击Scalar → Max → Value(取观察面上的磁场最大值);点击Input → Number → Scalar,输入0.015;点击Scalar → Log(求对数);点击Input → Number → Scalar,输入-20;点击General → *(相乘);即完成屏蔽效能的定义,然后点击上侧的Add,在Name栏输入dB,即将屏蔽下能表达式标记为dB,并保存。
右键单击工程树下的Optimetrics,选择Add → Parametric,点击右侧的Add,在Variable下选择屏蔽层厚度变量thick,在Start栏输入5mm,在Stop栏输入20mm,在Step栏输入3mm,即分析5mm:3mm:20mm的情况,然后点击中间的Add>>,添加扫描分析参数,然后点击OK。然后选择Setup Sweep Analysis下的Calculations选项卡,点击下面的Setup Calculations,在弹出的对话框中,将Report Type选为Fields,然后选择Quantity下的在Field Calculator下定义的dB,然后点击Add Calculation。
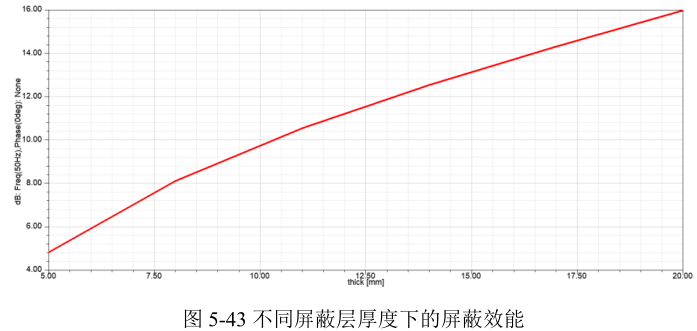
点击Analyze All,待计算完成后,右键单击工程树下的Optimetrics → ParametricSetup1,选择View Analysis Result,会弹出屏蔽效能与屏蔽层厚度的关系,如图 5‑43所示。
5.6.5附加损耗的计算
在增加屏蔽层后,屏蔽层上将产生涡流损耗,这部分损耗是由三相交流母线耦合过来的,因此一般称其为附加损耗,即因为屏蔽额外引入的损耗。
首先在场计算器中定义附加损耗,具体操作如下:右键单击工程树下的Field Overlays → Calculator:点击Input → Quantity → OhmicLoss;点击Input → Geometry → Volume → Shielding;点击Scalar → ∫(积分),然后将表达式定义为Pa并保存。
请同学们参考不同屏蔽层厚度下屏蔽效能计算的步骤,自行完成不同屏蔽层厚度下附加损耗的计算,计算结果如下。
本文章使用limfx的vsocde插件快速发布