MATLAB 回归分析

一元回归

命令	说明
p=polyfit(x,y,n)	对x、y进行n阶幂函数的拟合
[p,S]=polyfit(x,y,n)	结构体S可用作polyval的输入来获取误差估计值
[p,S,mu]=polyfit(x,y,n)	返回的mu(1)为mean(x)；mu(2)为std(x)

举例

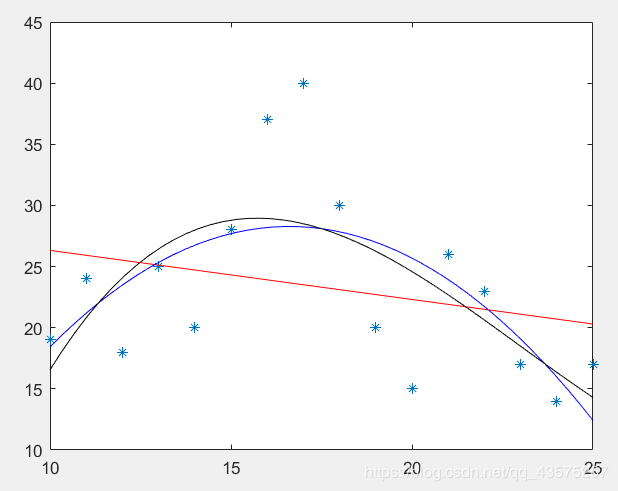
x = [10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25];
y = [19 24 18 25 20 28 37 40 30 20 15 26 23 17 14 17];
plot(x,y,'*');
hold on
y1 = polyfit(x,y,1);
f1 = poly2sym(y1);
y2 = polyfit(x,y,2);
f2 = poly2sym(y2);
y3 = polyfit(x,y,3);
f3 = poly2sym(y3);
fplot(f1,'r');
fplot(f2,'b');
fplot(f3,'k');
axis([10 25 10 45]);

在这里插入图片描述

多元线性回归理论

当有p个自变量$x_1,x_2,x_3,\dots$时，多元线性回归理论模型是 $y=b_1+b_2x_1+b_3x_2+\dots$
要进行回归分析，首先要构造矩阵X，矩阵X第一列都是1，用于求出上述式子中的b1。剩余的自变量，每个自变量的观测值排成一列。
返回的 b 是一个数组，即 $[ b_1,b_2,b_3,...]$

函数	说明
$b=regress(y,X)$	对因变量y和自变量X进行多元线性回归。
$b=regress(y,X,alpha)$	alpha指定置信水平
$[b,bint]=regress(...)$	bint是回归系数b的默认95%置信度的置信区间
$[b,bint,r]=regress(...)$	r为残差
$[b,bint,r,rint]=regress(...)$	rint为r的置信区间
$[b,bint,r,rint,s]=regress(...)$	s为四个参数指标，详见后文

举例

x1 = [43.1 49.8 51.9 54.3 42.2 53.9 58.6 52.1 49.9 53.5 ...
    56.6 56.7 46.5 44.2 42.7 54.4 55.3 58.6 48.2 51.0];
x2 = [29.1 28.2 37.0 31.1 30.9 23.7 27.6 30.6 23.2 24.8 ...
    30.0 28.3 23.0 28.6 21.3 30.1 25.6 24.6 27.1 27.5];
y = [11.9 22.8 18.7 20.1 12.9 21.7 27.1 25.4 21.3 19.3 ...
    25.4 27.2 11.7 17.8 12.8 23.9 22.6 25.4 14.8 21.1];
X(:,1) = (linspace(1,1,20))';
X(:,2) = x1';
X(:,3) = x2';
b = regress(y',X);
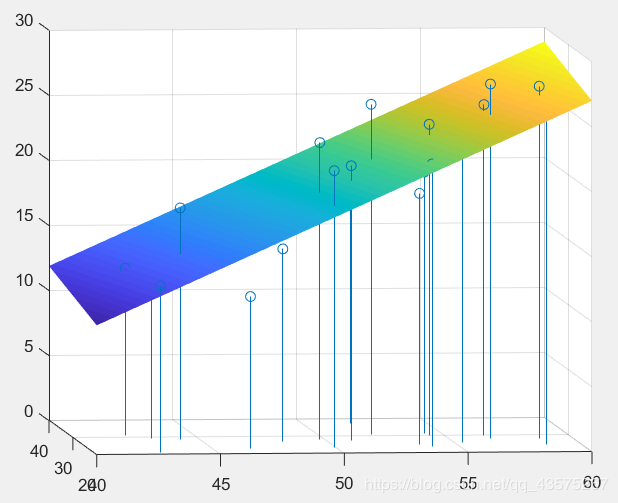
stem3(x1,x2,y,'o');
hold on
syms f(u,v)
f(u,v) = b(1) + b(2)*u + b(3)*v;
fsurf(f,'edgeColor','none');

在这里插入图片描述

如图可以直观反映实际值和理论值之间的关系。

多元回归分析建模

并不是所有的数据都可以用多元回归分析来建模的，在建模前，必须要用数据可视化来观察每个变量是不是都有较好的线性关系。
例如：我们对一组数据进行处理

x1 = [3.5 5.3 5.1 5.8 4.2 6 6.8 5.5 3.1 7.2 4.5 4.9 ...
    8 6.5 6.6 3.7 6.2 7 4 4.5 5.9 5.6 4.8 3.9];
x2 = [9 20 18 33 31 13 25 30 5 47 25 11 ...
    23 35 39 21 7 40 35 23 33 27 34 15];
x3 = [6.1 6.4 7.4 6.7 7.5 5.9 6 4 5.8 8.3 5 6.4 ...
    7.6 7 5 4.4 5.5 7 6 3.5 4.9 4.3 8 5.8];
y = [33.2 40.3 38.7 46.8 41.4 37.5 39 40.7 30.1 52.9 38.2 31.8 ...
    43.3 44.1 42.5 33.6 34.2 48 38 35.9 40.4 36.8 45.2 35.1];
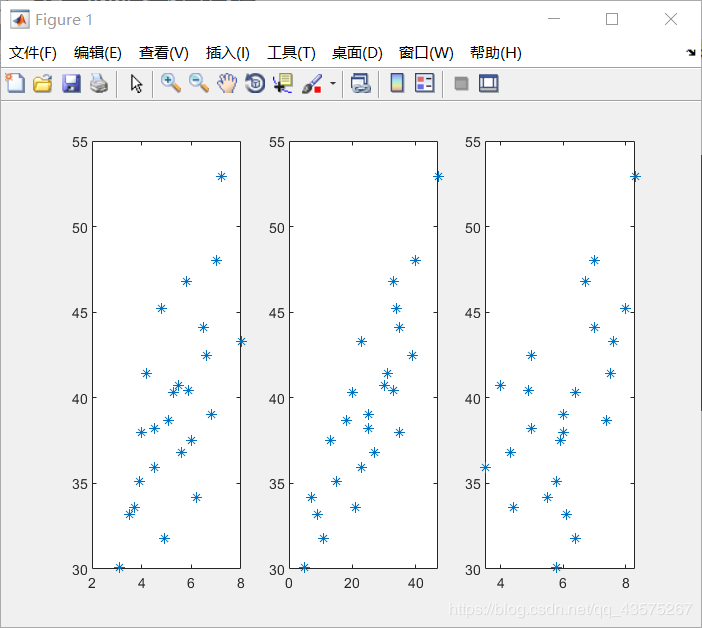
subplot(1,3,1); plot(x1,y,'*');
subplot(1,3,2); plot(x2,y,'*');
subplot(1,3,3); plot(x3,y,'*');

在这里插入图片描述

我们可以看到基本呈线性关系，所以可用多元线性回归问题来拟合。

X = [ ones(24,1),x1',x2',x3'];
[b,bint,r,rint,s] = regress(y',X,0.05);

结果检验
- 回归系数置信区间 $brint$ 不包含零点表示模型较好
- 残差 $r$ 在零点附近表示模型较好
- s 返回四个值，相关系数平方 $R^2$，假设检验统计量 $F$, $F$对应的概率 $p,s$
- 相关系数 $R$：R大表明线性相关性较强
- F 检验：应满足 $F>F_{1-\alpha}(m,n-m-1)$，其中 $\alpha、m、n$ 分别为设置的置信区间、因变量个数、因变量数据的个数。
- p：应满足 $p<\alpha$
- $s^2$：应越小越好，主要在建模改进时作为参考数据。

逐步回归

逐步回归会挑选一些具有代表性的变量，剔除一些不重要的变量
逐步回归命令：stepwise (X,Y, in, penter, premove)
- X 和 Y 与多元回归基本相同，不同点是：X、Y顺序相反，且逐步回归时，X第一列不要设为1，会自动算出常数项。
- in：给出初始模型中包含的子集，缺省时都不在模型中。
- penter：变量进入时，显著性水平，缺省值 0.05
- premove：变量剔除时，显著性水平，缺省值 0.10
当我们输入命令后，我们会打开一个 UI 界面，例如：

x11 = [7 1 11 11 7 11 3 1 2 21 1 11];
x12 = [26 29 56 31 52 55 71 31 54 47 40 66];
x13 = [6 15 8 8 6 9 17 22 18 4 23 9];
x14 = [60 52 20 47 33 22 6 44 22 26 34 12];
y1 = [78.5 73.4 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.9 113.3];
stepwise([x11',x12',x13',x14'],y1')

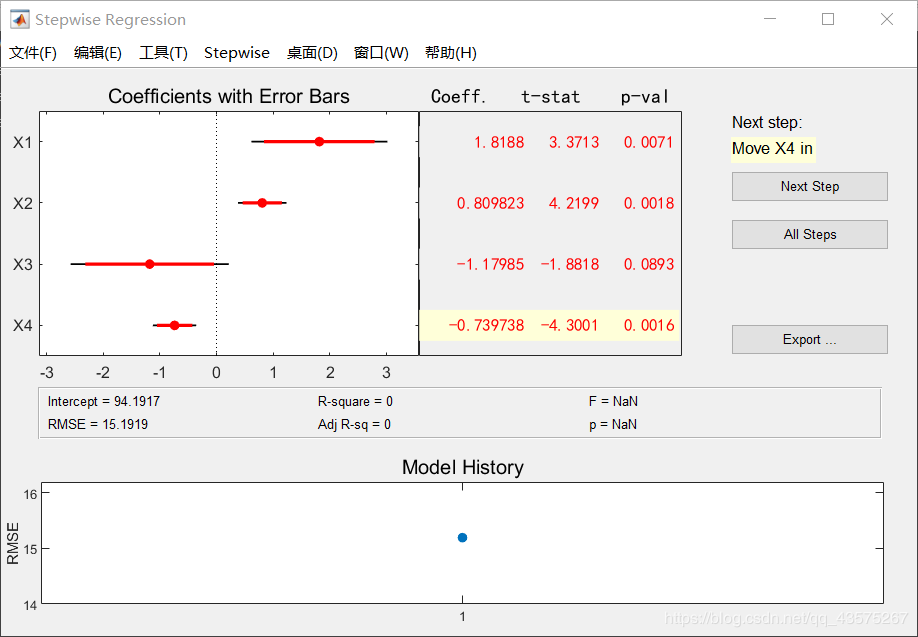
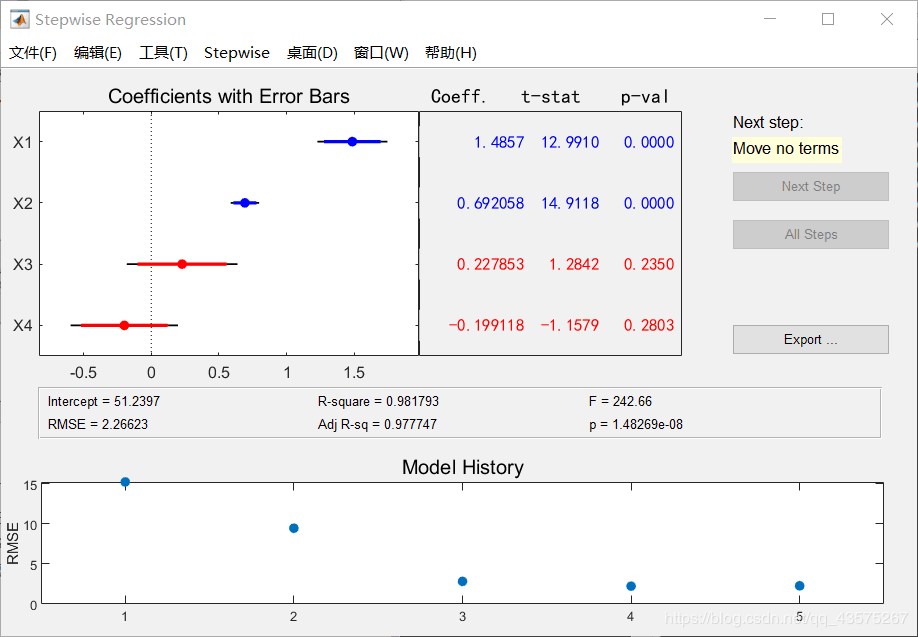
在这里插入图片描述

右侧 Next Step 表示进行下一步操作，All Step 表示一次性进行完所有操作。
我们的 in 默认所有变量不在初始模型中，所以我们现实 Next Step 是将 X4 放入模型，我们一直点击 Next Step 可以观察到模型建立的步骤是：加入X4、加入X1、加入X2、剔除X4。也就是说最终回归方程只有 X1、X2 两个变量。

在这里插入图片描述

用到的变量为蓝色，剔除的变量为红色。Coeff 即为回归系数。下方 Intercept 为常数项。
下方 R-square 为 $R^2$，Adj R-sq 为修正值 $R_\alpha ^2$，RMSE为残差均方。
判断回归效果和多元线性回归相同。

本文章使用limfx的vsocde插件快速发布

函数	说明
\(b=regress(y,X)\)	对因变量y和自变量X进行多元线性回归。
\(b=regress(y,X,alpha)\)	alpha指定置信水平
\([b,bint]=regress(...)\)	bint是回归系数b的默认95%置信度的置信区间
\([b,bint,r]=regress(...)\)	r为残差
\([b,bint,r,rint]=regress(...)\)	rint为r的置信区间
\([b,bint,r,rint,s]=regress(...)\)	s为四个参数指标，详见后文