3.1 基本理论

3.1.1 基本方程

我们在第二章说过，稳态情况下，电流J 为零对应的是静电场问题，电流J 不为零对应静磁场问题，但实际中存在一种特别情况，即当电流J 很小时，电流产生的磁场很弱，我们并不关心或对系统的电流分布基本无影响，这时我们或许可以忽略磁场，更关心电场分布。前面介绍静电场仿真时，我们假设了系统中无电流产生，电场由净电荷引起。但欧姆定律告诉我们，导电媒质在电场作用下将驱动电流，所以说，只有当媒质电导率小到可以忽略时，我们才能近似为静电场。另外，我们还可以从Maxwell方程看出，当系统的传导电流处于稳定状态时，电场和磁场相互不耦合，尽管传导电流很大，我们可能不关心磁场，而只关心电场。在以上几类问题中，我们都可以采用传导电流场分析，分直流传导场和交流传导场两种类型。我们知道，由Maxwell方程组中的磁场旋度方程和电场散度方程可以推导出电荷守恒定律

$\nabla\bullet J+\frac{\partial\rho_e}{\partial t}=0$ (3-1)

将电荷密度表示成电位移矢量的散度，有

$\nabla\bullet(J+\frac{\partial D}{\partial t})=0$ (3-2)

由欧姆定律有

$\nabla\bullet(\sigma E+\epsilon\frac{\partial E}{\partial t})=0$ (3-3)

对不包含感应电场的情况，

$E=-\nabla\varphi$ (3-4)

式化为电位形式

$\nabla\bullet(\sigma\nabla\varphi+\epsilon\frac{\partial\nabla\varphi}{\partial t})=0$ (3-5)

或

$\nabla\sigma\bullet\nabla\varphi+\sigma\nabla^2\varphi+\nabla\epsilon\bullet\frac{\partial\nabla\varphi}{\partial t}+\epsilon\frac{\partial\nabla^2\varphi}{\partial t}=0$ (3-6)

这就是传导电流场方程。

从方程(3-6)可以看出，当系统达到稳态时，方程可化简为直流传导方程

$\nabla\sigma\bullet\nabla\varphi+\sigma\nabla^2\varphi=0$ (3-7)

这与前面介绍的静电场方程十分接近。系统没有达到稳态时方程稍复杂，但一种稍简单的情形是时谐激励的情况，即有正弦激励产生的交流传导场，此时方程可化为

$\nabla\sigma\bullet\nabla\varphi+\sigma\nabla^2\varphi+j\omega\nabla\epsilon\bullet\nabla\varphi+j\omega\epsilon\nabla^2\varphi=0$

这就是所谓的交流传导场问题。

由式(3-7)和式(3-8)可知，电流场求解的自由度为电势，在完成传导场电势分析后，可算得电场分布及电流分布。值得我们注意的是，在交流传导分析中，严格地说，因有传导电流产生，必然会激励磁场，交变的磁场会反过来产生感应电场，叠加在原电场基础上影响电流分布，这在ANSYS交流传导分析中是没有考虑的。在第5章涡流场中我们将知道，在导体中交变电流存在趋肤效应，这是电磁感应现象造成的，这是就必须考虑磁场的作用。因此，ANSYS交流传导场分析仅适用于非良导体分析，主要用于介质损耗的计算。

目前，在ANSYS的传导场分析中，2D问题支持直流传导场和交流传导场问题的分析，但3D问题仅支持直流场分析。直流传导场分析的典型应用是导体直流欧姆损耗的计算，交流传导场分析的典型应用是介质的损耗分析。需要注意的是，在交流传导场中，所有场量均以复数的形式表示，关于场量的复数表示，具体可以查看第5章涡流场部分的相关介绍。

3.1.2 电流建立过程及弛豫时间

（1）电流的建立过程

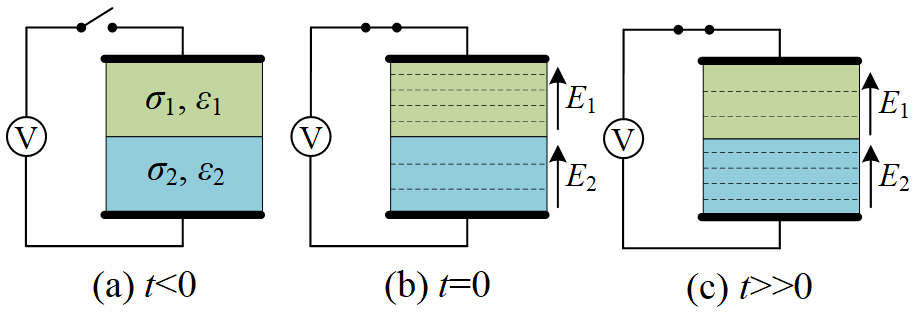
考虑如图3‑1(a)所示的电路结构，电极之间有两种介质，其中 $ε_1~>ε_2$ ， $σ_1<σ_2$ 。在t=0时刻（如图3‑1(b)所示），电路中的开关接通，此时，两电极上存在电势差，并在介质中产生电场，但此时介质中电流尚未建立，没有电流，也没有自由电荷。此时，两介质交界面应满足方程∇·D=∇·εE=ρ=0，即 $ε_1E_{n1}=ε_2E_{n2}$ 。即在电流建立之前的瞬间，介质中的电位分布完全由两个介质的相对介电常数决定，此时，可以采用静电场进行分析。

图 3‑1 传导电流的建立过程

当电流开始流动并达到平衡时（如图3‑1(c)所示），自由电荷将会在两介质的交界面积累，自由不再为零, $ε_1E_{n1}=ε_2E_{n2}$ 也不再满足。但是，此时介质内的电流密度满足∇·J=∇·σE=-∂ρ/∂t=0（因为已达到稳态），即 $σ_1E_{n1}=σ_2E_{n2}$ 。即在电流建立并达到稳态之后，介质内的电位分布主要由介质的电导率决定，此时，可以采用直流传导场进行分析。

（2）弛豫时间

从施加电压到电流达到平衡的时间常数称为弛豫时间，可表示为τ=ε/σ，对于良导体而言（比如铁， $ε=9×10^{-12}$ ， $σ=1×10^7$ ）， $τ=9×10^{-19}s$ ，即在合闸的瞬间便能达到平衡状态，此时可以直接采用直流传导场来进行分析。对于一些介质材料（比如熔凝石英， $σ=1×10^{-17}$ ），弛豫时间约为 $10^5s$ 量级，即电流达到平衡的时间非常长，此时可以采用静电场进行分析。对于介于二者之间的材料（弛豫时间与问题关注的时间尺度相当），则需要采用瞬态电场求解器进行完整的分析。

3.2 前/后处理方法

3.2.1 激励源

(1) 电压

电势是传导场所求解的自由度，因而电压是所有传导场分析中最常见的一种激励。目前，Maxwell的2D传导场分析中只支持电压激励。

(2) 电流

如果已知一个导体上的总电流，则可采用电流激励。电流激励一般需要配合电压激励或汇使用（但二者不可同时使用），相当于给计算提供一个参考电位，软件会自动计算导体内的电位分布。

(3) 汇

一般与电流激励配合使用，相当于是电流的汇合点。

3.2.2 边界条件

(1) 默认边界

在介质的交界面，默认法向电流密度J 连续，切向电场强度E 连续；在求解域的边界，默认为纽曼边界，即电流密度J 和电场强度E 均与边界平行。

(2) 对称边界（Symmetry）

与静电场分析类似，对称边界分为奇对称与偶对称：在偶对称（Even）中，电流密度J 和电场强度E 均与边界平行；在奇对称（Odd）中，电流密度J 和电场强度E 均与边界平行。

(3) 气球边界（Balloon）

与静电场分析中的气球边界类似，用于模拟近似无穷远边界。

(4) 绝缘边界条件（Insulating）

当两导体之间存在很薄的绝缘层时，为了计算导体内的电流场，必须把绝缘层考虑在内。如果单独对绝缘层建模，将会引起局部网格加密，增大计算量。如果我们不是特别关心绝缘层周围的电流分布情况，就可以利用绝缘边界来进行等效，而不必为绝缘层单独建模，这个用法与静电场中的绝缘边界很类似。目前，仅3D直流传导场支持绝缘边界条件。

(5) 电阻边界条件（Resistance）

当存在一个很薄（厚度远小于其他模型的尺寸）的电阻材料时，单独对其建模也会造成局部网格的加密，增大计算量。这时可以采用与绝缘边界类似的处理方法，即采用电阻边界条件模拟该薄层电阻，前提条件是该薄层电阻的电位是已知的（即该边界上电流只存在法向分量）。目前，仅2D直流传导场支持电阻边界条件。

(6) 主从边界条件（Master/Slave）

与静电场、静磁场等仿真中的主从边界类似，具体参见第4章静磁场中相关介绍。

3.2.3 电流的计算

电流的计算可以通过电流密度在表面上的积分得到，即

$I=\int_SJ\bullet dS$ (3-9)

其中，J=σE=-σ∇φ。需要注意的是，在2D平面（XY）分析中，积分得到的电流为Z轴方向上单位长度上的电流（电流在XY平面内），单位为A/m；在2D轴对称（RZ）分析中，计算得到的为总电流（即已经考虑了环向积分）。此外，还需注意的是，在交流传导分析中，电流是以复数形式表示的，关于场量的复数表示参见第五章相关内容。

3.2.4 损耗的计算

损耗的计算可以通过焦耳热功率密度对体积的积分得到，即

$P=\int_VE\bullet JdV$ (3-10)

在Maxwell场计算器中，焦耳热功率密度E·J 被标记为Ohmic Loss.

3.3 案例1——直流隔离开关的损耗计算

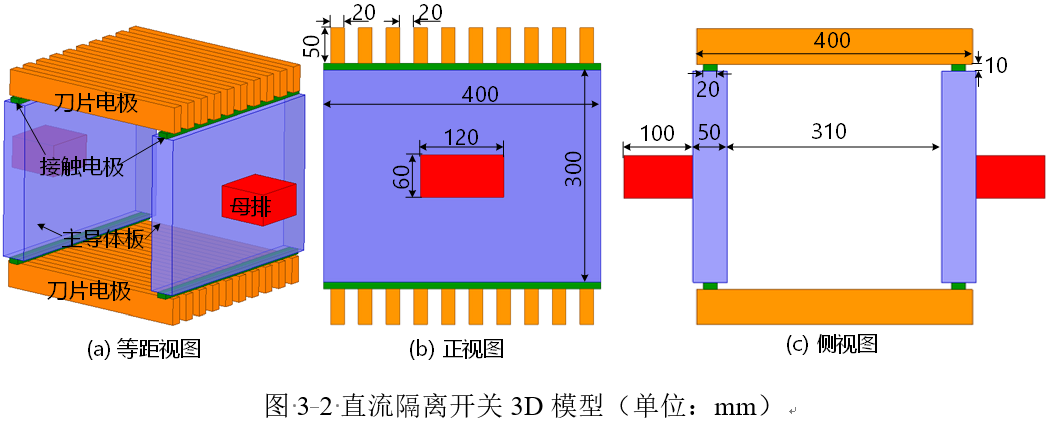
隔离开关是常用的电力设备，在电力系统、工业中有广泛的应用。隔离开关就有承载电流、隔离电压的作用（注意隔离开关不是断路开关，不能分断电流），主要用于系统检修时与电源的隔离，保证安全。隔离开关有交流和直流两大类，图3‑2所示为典型的刀片式直流隔离开关3D模型，主要由刀片电极、接触电极、主导体板和母排组成（除此之外还包含驱动刀片电极开合的电机等辅助部件）。刀片电极一般由铜制成，且构成阵列，以降低与接触电极之间的接触电阻（本案例中不考虑接触电阻）。接触电极用于与刀片电极的接触，一般由铜制成，且在表面镀银，以保证较低的接触电阻。主导体板是整个开关的主要支撑结构，为降低成本，一般用铝制成。母排主要用于开关的安装，同时用于与主回路的连接，一般多采用铝制成。假设该开关的额定运行电流为10kA，试计算该开关额定运行时的欧姆损耗功率。

图 3‑2 直流隔离开关3D模型（单位：mm）

3.3.1 本节知识点

3D对称性的使用
云图的编辑与美化
直流损耗的计算

3.3.2 分析模型的建立

（1）确定分析类型

分析这个问题可知，模型不能采用2D等效，因此是一个3D直流传导场问题。点击Insert Maxwell 3D Design图标，新建一个3D仿真任务，然后点击工具栏Maxwell 3D → Solution Type，弹出新的对话框中，求解器选择DC Conduction。

（2）建立分析模型

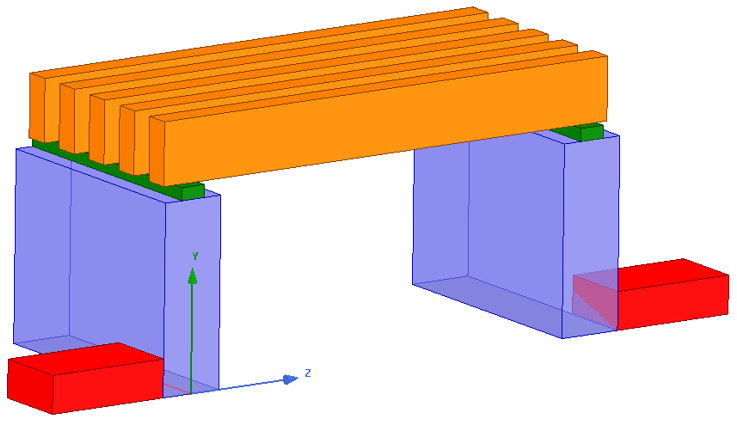
观察图3‑2所示的模型可知，该模型具有很高的对称性，可以采用1/4甚至1/8模型进行简化。这里我们采用1/4模型，在电流传导方向上，我们不做对称简化，以保留电流传导路径的完整性，方便我们观察计算结果。根据图3‑2所示的模型参数，创建1/4分析模型，如图3‑3所示。建模过程中，相同的几何模型可以尽量采用复制操作（EditEdit →Duplicate → Along Line/Mirror）来简化建模的过程。具体建模过程请自行完成，或者参考文献[1]相关内容。需要注意的是，对于直流传导场而言，导体电导率远大于空气（几十个数量级），因此无需创建Region。

图 3‑3 直流隔离开关1/4仿真模型

（3）设置材料属性

将母排和主导体板的材料设置为铝（Aluminum），将接触电极和刀片电极的材料设置为铜（Copper）。

（4）网格划分

直流传导场对网格的要求不高，将刀片电极的网格尺寸设置为30mm，将接触电极的网格尺寸设置为20mm，将主导体板的网格尺寸设置为50mm，将母排的网格尺寸设置为30mm。

（5）施加载荷与边界条件

载荷的施加比较简单，在一端母排的端面施加电流激励，电流为总电流的1/4，即2.5kA，在另一端母排的端面施加电压激励（只是提供一个参考电位，理论上施加任何电位均可，一般设置为零）或者汇（Sink）。对于边界条件而言，在使用了对称的面（图3‑3中的XZ平面及YZ平面）施加偶对称（Even, Flux Tangential），其实也可以不加对称边界，因为软件模型的边界条件也是场线平行与边界，与偶对称相同。

（6）求解设置

将计算精度设置为0.1%，点击Validate检查设置，确认无误后开始计算。

计算结果的处理与分析

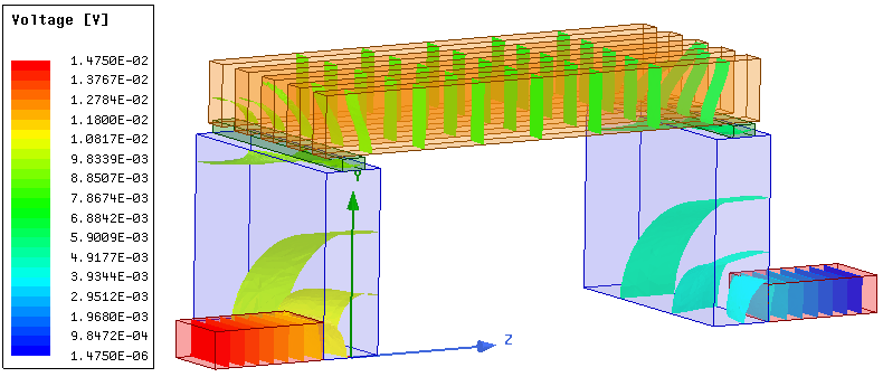
计算完成之后，可以先通过一些简单的场分布云图初步检查计算结果。选中所有模型，单击右键选择Fields → Voltage，将给出所有导体中电位等值面分布。为了方便观察，可以将模型改成透明的，具体操作是：在模型树下选择相应的模型，单击右键选择Properties，在弹出的对话框中将Transparent栏修改为0.8（即透明度改成80%）。此外，Maxwell中默认的云图只有15个值，即将得到的场值按最小值到最大值均分为15份按云图显示。为了方便观察，可以双击图形窗口左上角的图例，在Scale选项卡下将Num. Division中的数据改成30，得到的电位分布图如图 3‑4所示。

图 3‑4 隔离开关电位分布图

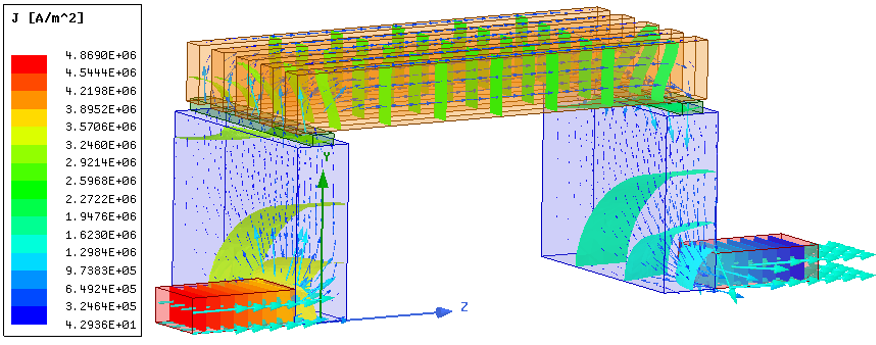
此外，我们还可以画出导体中电流密度矢量分布。选中所有模型，单击右键选择Fields → J → J_Vector，将给出所有导体中电流密度矢量分布。如果画出的矢量箭头较小，可以对其进行编辑。双击图形窗口左上角的图例，打开Marker/Arrow选项卡，调整Arrow Options下的Size即可调整矢量箭头的大小。得到的电流密度分布云图如图 3‑5所示，其中箭头方向代表电流传导方向，箭头的长短和颜色代表电流密度的大小。

图 3‑5 隔离开关电流密度矢量分布（Map Size）

如果我们并不关心电流密度大小的分布，只关注电流矢量的方向，此时可以将Arrow Options下的Map Size勾选掉，得到的分布图如图3‑6所示。此时所有箭头长度相同，不能反映电流密度的大小，但能更方便观察结果，电流密度的大小可以通过箭头的颜色大致判断。

图 3‑6 隔离开关电流密度矢量分布（非Map Size）

基于上述场量分布，结合电磁场相关知识，我们大致可以判断，计算应该无误。接下来就可以来计算开关的损耗了。右键单击工作树下的Field Overlays，选择Calculator，接下来的操作如下：Input → Quantity →OhmicLoss，再选择Input → Geometry → Volume → AllObjects，再选择Scalar → 积分（∫），最后点击Output → Eval，计算得到的损耗为36.9W，即隔离开关总损耗为147.6W。当然也还可以使用E·J 的体积分进行计算，有兴趣的同学可以自己尝试。

3.4 案例2——高压同轴电缆的介质损耗计算

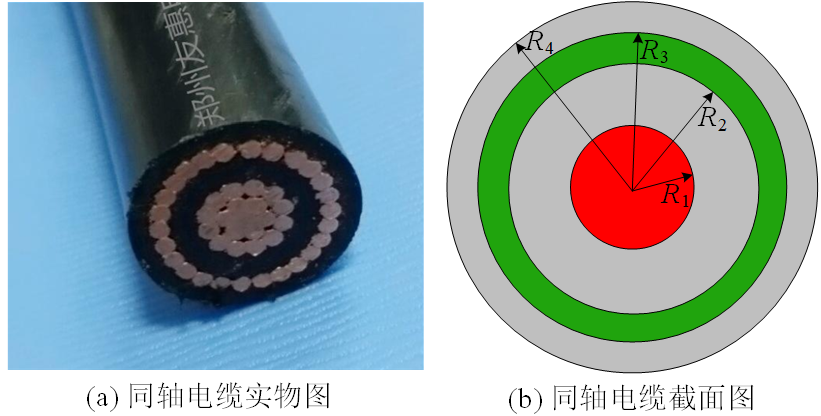
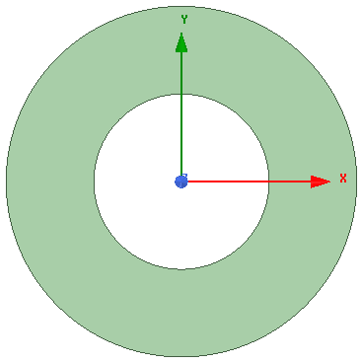
同轴电缆是一种往返导体同轴布置的特殊电缆结构（如图3‑7所示），内、外导体电流大小相同，方向相反，对外不会产生磁场，因为具有良好的电磁兼容性能，在电力系统和通讯等领域有着广泛的应用。考虑如图3‑7所示的同轴电缆，假设内导体半径 $R_1$=5mm，内绝缘层外半径 $R_2$=10mm，外导体外半径 $R_3$=13mm，外绝缘层外半径 $R_4$=16mm，绝缘介质的相对介电常数为10，电导率为10S/m（实际上绝缘介质的电导率要比这个值小得多，但设置的太小Maxwell似乎算不出电流分布），电缆工作电压为10kV，计算工频下该电缆的介质损耗。

图 3‑7 同轴电缆示意图

3.4.1 本节知识点

长直模型的2D简化
基于边界条件的模型简化
介质损耗的计算

3.4.2 分析模型的建立

（1）确定分析类型

由于电缆的长度相对于其截面可认为是无限长，因此可认为电缆为长直模型，可以采用2D平面模型简化。点击Insert Maxwell 2D Design图标，新建一个2D仿真任务，然后点击工具栏Maxwell 2D → Solution Type，在Geometry Mode栏选择Cartesian, XY（平面模型，区别于轴对称RZ模型），求解器选择AC Conduction。

（2）建立分析模型

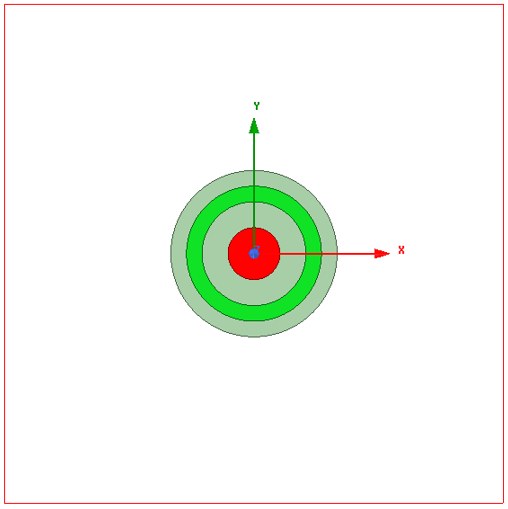
该仿真模型的建立比较简单，首先建立4个同心圆，然后分别利用Edit → Boolean → Subtract操作得到所需的模型。需要注意的是，Subtract操作对话框中，Blank Parts栏应为大模型，Tool Parts栏应为小模型（被减掉的模型），同时可以勾选下方的Clone tool objects before operation，即在减法操作完成之后还保留被减掉的模型，避免重复创建相同的模型。最后为模型创建一个Region，Percentage Offset设置为100。

图 3‑8 同轴电缆2D仿真模型

（3）设置材料属性

将内、外导体的材料设置为铜（Copper）。对于绝缘介质，选择绝缘介质模型，单击右键选择Assign Material，在弹出的材料设置界面点击下方的Add Material，新弹出的编辑材料对话框中，在Material Name栏输入Dielectric，在Relative Permittivity栏输入10，在Bulk Conductivity 输入10，即完成我们自己的介质材料的定义，并赋给我们的仿真模型。求解域材料采用默认。

（4）网格划分

两电极之间的区域场梯度最大，网格可以设置的相对密集，网格尺寸设置为2mm；内、外导体为等势体，可以不设置网格，或者设置一个相对较粗的网格，如5mm；外绝缘层网格尺寸设置为3mm；求解域网格设置为8mm。

（5）施加载荷与边界条件

载荷比较为简单，在内、外导体上分别施加10kV和0V，在最外层边界这是balloon边界条件。

（6）求解设置

将计算精度设置为0.1%，然后点击Solver选项卡，将Adaptive Frequency修改为50Hz（默认值为60Hz，美国的工频频率），设置完成后点击Validate检查设置，确认无误后开始计算。

（7）后处理

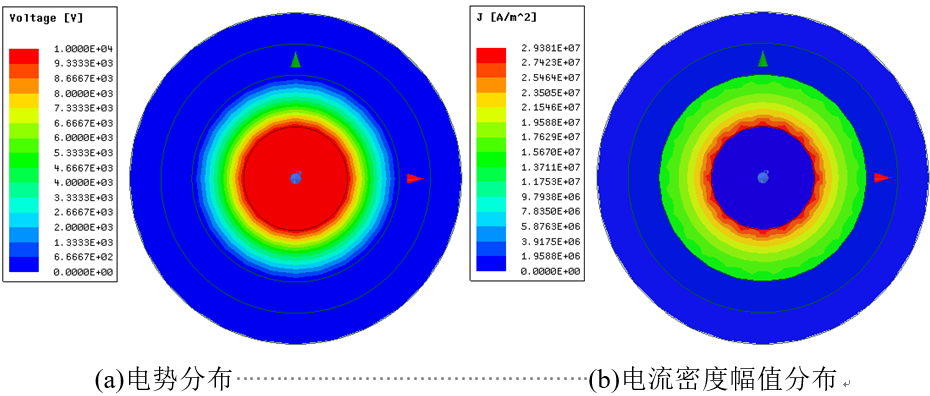
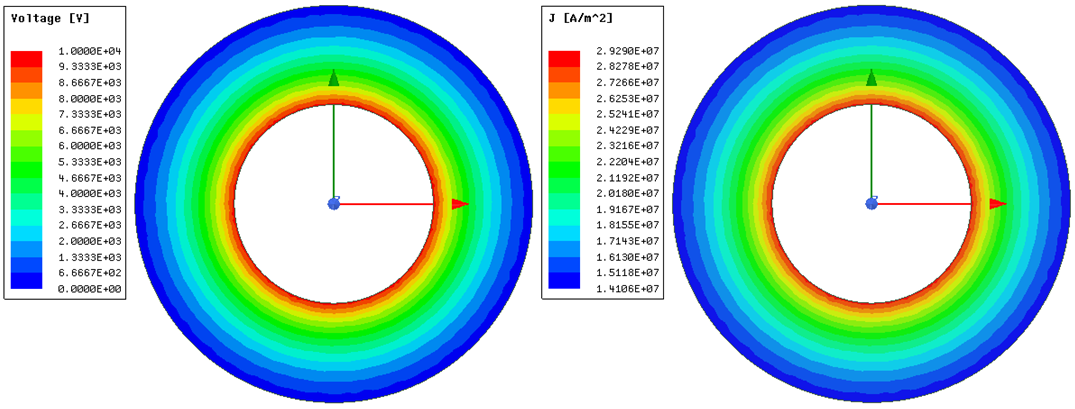
计算完成之后，可以先通过一些简单的场分布云图初步检查计算结果。选中除Region之外的所有模型，单击右键选择Fields → Voltage 和Fields → J → Mag_J，将分别给出所有模型中电势和电流密度幅值分布，如图 3‑9所示。

(a)电势分布 (b)电流密度幅值分布

图 3‑9 全模型电势分布及电流密度幅值分布

由计算结果可知，电势梯度即电场只存在于内绝缘介质中，那么电流也只分布在内绝缘介质中，其他部分没有电流的分布，这比较好理解，虽然内、外导体为良导体，但在仿真中，二者均为等势体，而电流是由电场即电势梯度驱动的，故而内、外导体中并不存在电流密度分布。

3.4.3 基于边界条件的模型简化

由于电流只集中于内绝缘介质，基于此，是否可以将模型进行简化呢？答案是肯定的。对于内绝缘介质而言，其两边的边界条件均已知，即外部的模型及其他边界条件对其计算不会有任何影响，因而在建模是可以只对内绝缘介质进行建模，并在其内、外边界上施加相应的电压激励即可，其他的模型均可不用建模。简化后的模型如图3‑10所示，只存在内绝缘介质模型。

图 3‑10 基于边界条件简化后的仿真模型

模型修改完成后，在绝缘介质的内、外边界上分别设置10kV和0V的激励电压，网格设置与求解设置均与全模型相同，然后开始计算。