2. 静电场数值模拟
2.1 基本理论
根据电磁场理论,引起电磁场的场源主要有净电荷、电流、永磁体,如果所讨论的系统中电磁场达到了稳定状态,同时系统中也没有永磁体,也无电流产生,那么这时的场源是由静电荷产生,我们称为静电场问题。从Maxwell方程组
\(\nabla\times E=-\frac{\partial B}{\partial t}\)
\(\nabla\times H=J+\frac{\partial D}{\partial t}\)
\(\nabla\bullet D=\rho_e\)
\(\nabla\bullet B=0\) (2-1)
可以看出,电场和磁场相互耦合("电生磁、磁生电"),但是如果系统达到了稳态, \(\partial/\partial t=0\) ,方程组将解耦为电场方程组和磁场方程组,两者互不影响。电流J 为零对应的是本章要讨论的静电场问题,电流J 不为零对应后面要讨论的静磁场问题。
对静电场问题,Maxwell方程组可以简化为
\(\nabla\times E=0\)
\(\nabla\bullet D=\rho_e\) (2-2)
实际上,有些时候尽管系统的电场处于变化状态,但根据我们的知识可以判断出Maxwell方程组中的位移电流项 \(\partial D/\partial t\) 对我们的分析认识造成的影响很小时,我们也可以将忽略掉位移电流项,将其看作静电场问题来求解,这是尽管电场是变化的,但是约束方程跟静电场一样,我们同样可以用静电场的方法求解。
从方程(2-2)可以看出,如果已知空间中任一点的电荷密度,解方程就可得到电位移矢量分布或电场分布。已知电场的散度和旋度,理论上求解是没什么问题的,但实际求解中有一点比较麻烦,方程 \(\nabla\bullet D=\rho_e\) 为矢量方程,每个方程实际上有3个分量,而且旋度运算比较复杂,所以并不太好求解,但是我们注意到,E 的旋度为零,这意味着它一定可以写为一个标量函数的梯度形式,这就是我们所说的电位φ。
\(E=-\nabla\varphi\) (2-3)
那么方程 \(\nabla\bullet D=\rho_e\) 可以化为
\(\nabla\bullet(\epsilon\nabla\varphi)=-\rho_e\) (2-4)
进一步化为
\(\epsilon\nabla^2\varphi+\nabla\epsilon\bullet\nabla\varphi=-\rho_e\) (2-5)
关于电位φ的方程为标量方程,求解更加方便,ANSYS的电磁模块的静电场求解都是以电位为待求变量的。
ANSYS对方程的求解采用的是有限元方法,这是一种在工程和科学研究应用十分广泛的微分方程数值解法,具体原理非本课程覆盖范围,感兴趣的读者可以参考相关书籍。
2.2 前/后处理方法
这里介绍几个与ANSYS求解电场问题直接相关的几个问题。
2.2.1 激励源
激励源在ANSYS工程管理窗口的Excitations中设置,打开可以看见共有电位Voltage、电荷Charge、悬浮Floating和体电荷密度Volume Charge Density几种设置,下面一一介绍。
(1)电荷(Charge)
我们知道静电场是由净电荷产生的,如果我们知道空间电荷密度分布,自然可以求得电位及电场分布,这对应ANSYS中的体电荷密度激励。这种设置在实际计算中使用不太多,主要因为电荷密度并不是一个容易测量的物理量,同时电荷密度分布会受到电场分布的影响,往往并不是一个独立的量。
(2)电荷密度(Charge Density)
电荷密度激励是一种有很强限制的激励,相对弱一点的是电荷激励,即限制某个区域的电荷总量,而不是电荷密度分布。有些时候我们知道某个物体上的总电荷量,要求周围电场分布,这时我们可以用电荷激励条件。
(3)悬浮(Floating)
悬浮条件用于与其它物体无直接电气连接的某个物体,该物体处在电场环境中,可能本身携带有净电荷,也可能只是在电场作用下感应局部电荷。比如置于电场环境中的金属小球,携带总电荷为零,但球体表面却带有电荷,正是这部分电荷与外加电场产生的合成电场形成的电场屏蔽,这部分感应电荷也将影响外部电场分布,所以我们也是要关注的。
(4)电位(Voltage)
电位激励是我们最常见的,即限制某物体一般是导体的电位为确定值,很容易理解。
2.2.2 边界条件
静电场分析中的边界条件主要有气球边界Balloon、绝缘边界Insulating、对称边界Symmetry、主从边界Master/Slave几种。
(1)气球边界条件(Balloon)
气球边界一般用于模拟近似无穷远边界,一般施加在仿真区域的边界,边界上场线与边界既不平行也不垂直。
(2)绝缘边界条件(Insulating)
绝缘边界条件严格来说并不算边界条件,一般用于仿真模型的简化。具体地说,如果某两个物体处于不同电位,但两者之间存在一个狭窄的缝隙,这将给网格划分带来很大麻烦,会导致狭缝处网格数剧增,然而我们往往并不关心狭缝中的电场分布,这时我们可以干脆把两个物体连接在一起,为了阻断两者之间的电气连接,在交界面上设置绝缘边界条件,这对狭缝外电场计算是一种很好地近似。绝缘边界条件也用于同一个物体上的裂纹,仿真时可将裂纹连接起来,而将连接界面设置为绝缘边界条件,这样既能保证裂纹两边绝缘,同时也不至于在裂缝处形成大量的细分网格。
(3)对称边界条件(Symmetry)
对称边界条件用于模型具有一定对称性的情况,比如,模型在几何及激励上都满足左右对称或上下对称,那么计算出来的场量分布就一定满足相应的对称性,建模时就不需要建立完整模型,而只需建立1/2、1/4甚至1/8模型,通过对称面上的场量约束可实现模型"自动补全"的效果。对称边界有奇对称和偶对称两种,电场矢量垂直穿过对称面(电位在对称面为常数)时为奇对称,电场矢量平行于对称面时为偶对称。使用对称边界可以有效减小模型的大小,大幅减小网格数目,后面将通过案例进行说明。
(4)主从边界条件(Master/Slave)
Master/Slave边界条件也被称作主从边界条件,它们总是一主一从配对使用的。工程实际中的模型除了可能具有前述对称性以外,还可能存在周期性(尽管不对称),如旋转电机的几何结构和激励在圆周上总是周期性重复的。这时我们可以利用主从边界条件来减小计算量。具体设置方法和案例我们放到磁场仿真章节介绍。
2.2.3 网格剖分
ANSYS具有自动网格剖分功能,也就是说,我们如果不限制网格方法,软件会自动根据计算误差要求进行剖分,而且计算过程中会不断调整,直到计算结果满足计算误差要求或达到最大计算次数为止(当然这里的满足计算误差要求是一个范数概念,即在某种全局衡量方法下满足要求,并不代表每个点的误差都很小),这就是所谓的自适应网格剖分。静电场分析对网格剖分没有特殊要求,做一些简单的网格参数设置即可,具体内容参见案例。
2.2.4 电场能计算
电场计算完成后,我们往往需要对结果进行一些后处理,如,计算电场强度分布、部件之间的电容、系统储存的电能、部件之间的电场力等。首先介绍电场能的计算。根据电磁场理论,电场能为
\(W_e=\frac{1}{2}\int_VE\bullet DdV\) (2-6)
所以要求某个物体内存储的电场能,只需要将其上的电场强度和电位移矢量点乘并积分就可得到,这可在场计算器中实现,在Maxwell经典产分析中内置的电场能量密度E·D/2表达式标记为Energy,在后处理中可以直接使用。
值得注意的是,ANSYS中二维计算中的积分包含XY积分和RZ积分两种,它们有什么区别呢?
首先为什么有两种积分呢?我们知道ANSYS仿真本身就包含笛卡尔二维坐标和柱坐标两种,在笛卡尔坐标系下的积分是很直观的,没什么特别之处,但柱坐标系下却稍复杂一些,比如图2‑1所示矩形,假如我们要求矩形(实际上为圆柱管)中储存的电场能大小,我们需要作积分
\(W_e=\frac{1}{2}\int_A(E\bullet D)Rd\theta dRdZ\) (2-7)
可以看出,这个积分并不是简单的将E 点乘D 在矩形上积分,而是要乘上R因子,这就是RZ积分。实际上ANSYS中的RZ积分的结果为在整个圆周上积分得到的结果。
换一种情况,如果我们要求流过矩形截面上的电流大小(虽然静电场中不求电流),那么我们要做积分
\(I=\int_AJ\bullet dS=\int_A J_\theta dRdZ\) (2-8)
可见这里并不需要乘上R因子,这就需要用XY积分。
体积分、面积分和线积分都有RZ积分和XY积分的差别,这里所举的两个例子,一个是体积分,一个是面积分,这本身就有差别,这需要我们在选择积分对象时分别选为体和面。
图 2‑1 二维轴对称模型下的矩形
2.2.5 电容矩阵
在电场作用下,任意两个不等电位的物体之间都有电容的概念,但是由于绝缘体上不同部位电位各不相同,定义电容的意义不大,所以电容一般定义于导体之间。导体间的电容反映了导体间电位变化与导体上电荷之间的关系,通常用一个矩阵表示,矩阵元素常被称为自电容和互电容。下面我们来看电容矩阵元素的含义。
如图2‑2所示的N个导体,导体电位为 \(V_i\)(i=1~N),导体带有电荷 \(Q_i\) ,每个导体与参考地之间的电容为 \(C_i\) ,两个导体之间的电容为 \(C_{ij}\) ,则有 
化为矩阵形式为
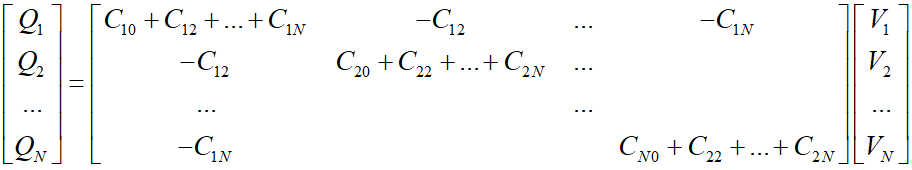
ANSYS软件静电场计算中设置Parameters中的Matrix里的电容矩阵就是上面反映电荷与电位关系的矩阵。为了计算电容矩阵中各元素的值,软件中可以依次将 \(V_1\) 至 \(V_N\) 设为1V,而其余导体全部设为0V,计算完电场后计算每个导体上的电荷,可以解出电容矩阵。
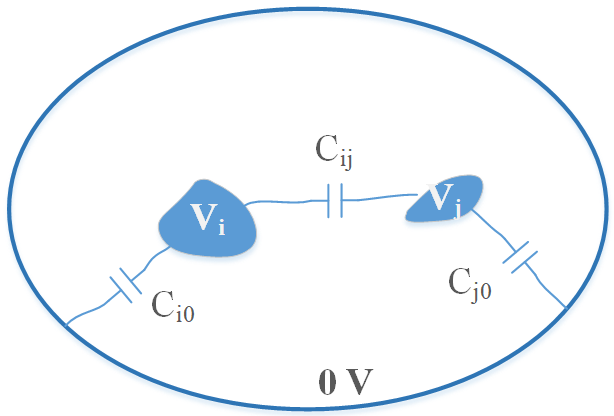
ANSYS软件中往往是通过另外一种方法计算的,下面简单介绍一下。我们知道,某一点电位可看作是系统中单个导体独立激励的电场的线性叠加,也就是说分别将导体i电压设为 \(V_i\) ,其它导体设为0,将所有情况下电位值叠加就可得到最终结果。系统中的电场能量为
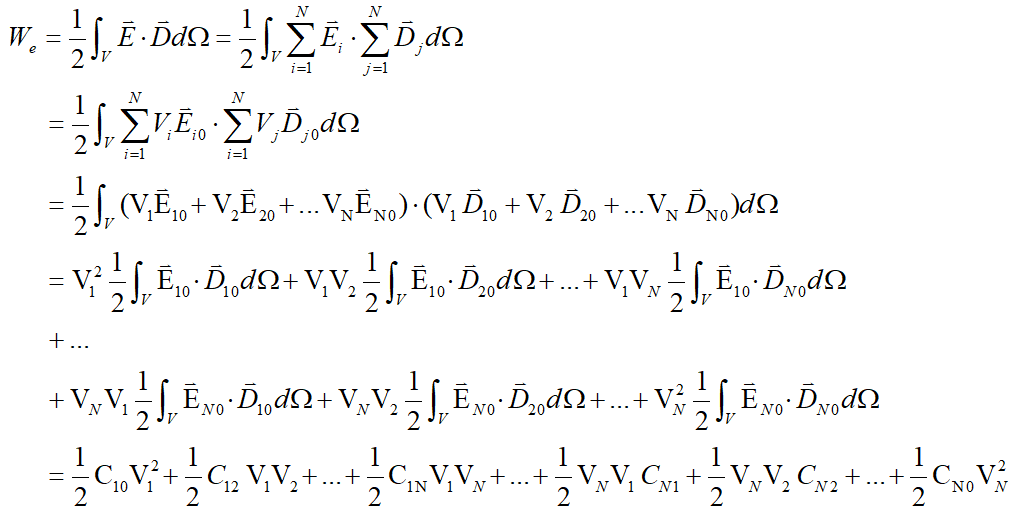
可见,
\(C_{ij}=\int_VE_{i0}\bullet D_{j0}d\Omega\) (2-12)
当i≠j 时, \(C_{ij}\) 表示导体间的互电容,当i=j 时, \(C_{ij}\) 表示 \(C_{i0}\)+\(C_{i1}\)+...+\(C_{iN}\) ,即电容矩阵中的对角元素。式中, \(E_{i0}\) 代表第i个导体加1V电位其它导体设为0V时任意位置的电场强度, \(D_{j0}\) 代表第j个导体加1V电位其它导体设为0V时任意位置的电位移矢量。
2.2.6 电场力/力矩
在Maxwell中,电场力和电场力矩的计算分为两种,分别介绍如下。需要注意的是,默认情况下Maxwell不会计算电磁力和电磁力矩,如果需要计算,需要在工程树下右键Parameters → Assign → Force/Torque进行设置,计算完成后在Solution Data下的Force/Torque选项卡查看计算结果。
计算电场力的第一种方法是计算自由电荷在电场作用下的受力,即
\(F=\int_V qEdV\) (2-13)
其中,q为电荷密度,E为电场。需要注意的是,上式中的q为自由电荷,因此不适用于介电常数大于1材料的电场力的计算(有极化电荷对电场力的贡献)。
一种各位准确的计算电场力的方法是采用虚位移法,即假设被分析对象存在一个很像的位移dx,计算系统电场能的变化dU,可认为系统能量变化是由电场力做功产生的,则电场力可以表示为
\(F=\frac{dU(v,x)}{dx}\mid_{V=constant}\) (2-14)
需要注意的是,利用虚位移法计算受力需要被分析导体为等势体,一般而言,在静电场分析中,导体都可以视为等势体,如果只是计算单个导体受到的电场力,这个条件可以很容易满足。
静电力矩由下式计算,即
\(T=\int_V q(r\times E)dV\) (2-15)
与式相同,上式并不适用于相对介电常数大于1的材料的电场力矩的计算。虚位移力矩的计算与虚位移力相似,即假设被分析绕旋转轴存在一个很小的旋转角度dθ,计算系统的能量变化dU,则物体受到的力矩可表示为
\(T=\frac{dU(v,\theta)}{d\theta}\mid_{V=constant}\) (2-16)
2.3 案例1——平板电容器
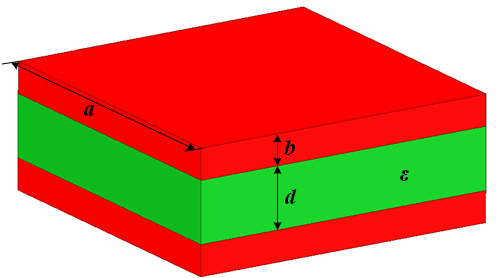
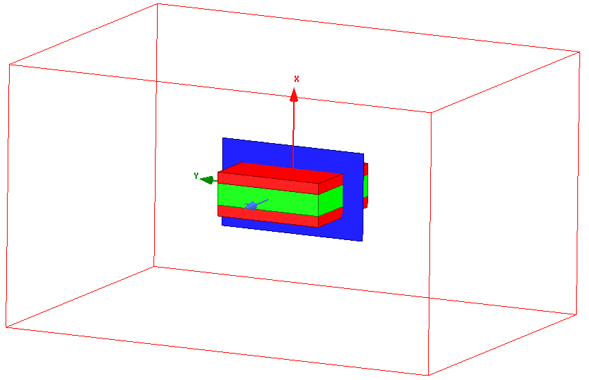
电容器是电子电路系统中基本元件之一,其仿真计算就是一个典型的静电场问题。工程上的电容器材料和形状各异,有薄膜、陶瓷、电解液、油等多种介质,有圆柱形、矩形等多种形状,平板电容可以看作其基本单元。这里我们来仍以图1‑1所示的平板电容器为例,介绍ANSYS静电仿真的基本方法,这里假设电容边长a=10mm,极板间距d=2mm,金属板厚b=1mm,介质的相对介电常数 \(ξ_r\)=10。
图 2‑3 平板电容器三维模型
2.3.1 本节知识点
参数化建模与参数化网格
电容的计算
求解域尺寸的选取
3D对称性的使用
2.3.2 分析模型的建立
(1)确定分析类型
分析这个问题可知,模型为长方体,并不具备旋转对称性或无穷长的特点,不能采用2D模型等效,因此可以确定为是一个3D静电场问题。点击InsertMaxwell 3D Design图标,新建一个3D仿真任务,然后点击工具栏Maxwell 3D →Solution Type,弹出新的对话框中,求解器选择Electrostatic。
(2)建立分析模型
在建模之前,为了实现建模的参数化,需要在Maxwell中定义模型参数变量。点击Maxwell 3D → Design Properties,点击Add...,在Name栏输入a(即电容器边长),在Unit Type栏选择Length(即单位类型选择为长度),Units栏采用默认的mm单位,Value栏输入10,即完成电容器边长的定义。采用同样的方法定义极板间距d和极板厚度b,再定义一个求解域建模相关的参数ratio1(即比例,无单位,取为100)。
首先创建下极板,点击Draw Box,用鼠标在绘图窗口随便点击+拖拽生成一个长方体,双击打开模型树Model → Solids → Vacuum(建模后的实体一般默认的材料属性为真空)→ Box1下的CreateBox,在Position(长方体的一个顶点)栏输入-a/2,-a/2,-d/2-b,在XSize栏输入a,在Ysize栏输入a,在Zsize栏输入b,即实现第一个极板的建模参数化。对于上极板,起点坐标和尺寸分别定义为(-a/2,-a/2,d/2)和(a,a,b),对于电介质,起点坐标和尺寸分别定义为(-a/2,-a/2,-d/2)和(a,a,d),这样就得到了中心在坐标原点的仿真模型。建模完成之后,分别将得到的三个实体命名为Plate_up(上极板)、Dielectric(电介质)和Plate_down(下极板),双击对应的实体模型,或者右键单击选择Properties选项,还可以对模型的颜色进行编辑。
图 2‑4 电容器仿真模型
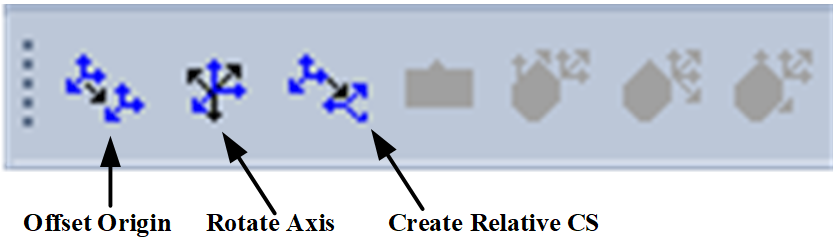
为了方便观察电容器周围的电场分布,我们还需要创建一个专门的观察面。在3D模型中,平面模型只能在XY平面内创建,为了得到电容器的一个侧向截面(如图2‑4所示的YZ平面),我们需要对坐标系进行旋转操作,即将XY平面旋转到YZ平面。这里介绍一下Maxwell里面关于坐标系的一些操作,Maxwell中关于坐标系常用的操作如图2‑5所示,需要说明的是,任何一个坐标系操作完成之后都会创建出一个新的局部坐标系(RelativeCS)。坐标平移(Offset Origin)比较简单,点击Offset Origin工具后,直接在右下角对话框中输入新的原点坐标即可,也可以在绘图窗口随便点击生成一个坐标系,然后双击模型树下Coordinate Systems → RelativeCS1(即刚刚生成的局部坐标系),修改Origin栏下的坐标值。
图 2‑5 Maxwell中常用的坐标系操作
坐标轴的旋转(Rotate Axis)相对复杂一点,其基本顺序是先确定新坐标系下的X轴,再确定Y轴,对于如图2‑4所示的坐标系,如果我们要将XY平面旋转到YZ平面,可以认为是将X轴旋转至Z轴,Y轴位置保持不变,即X轴的坐标为(0,0,1),Y轴的坐标为(0,1,0)。点击Rotate Axis工具之后,右下角会坐标输入窗口,这个是用来确定X轴坐标的,输入(0,0,1)即可,按Enter后,会出现新的坐标输入窗口,这个是用来确定Y轴坐标的,输入(0,1,0)即可,当然也可以先随便点击再修改坐标系属性。如果想将坐标系绕Z轴旋转一个角度θ,则X轴的坐标就是(cos(θ),sin(θ),0),Y轴的坐标是(-sin(θ),cos(θ),0),其他的旋转可依此类推。创建局部坐标(Create Relative CS)的操作其实就是上述两个操作的组合,即先确定坐标原点,再分别确定X和Y轴,这里不再赘述。
坐标旋转完成之后,即可创建观察面,观察面端点坐标取为(-3d/2-b,-a/2-d,0),各向的长度取为(3d+2b,a+2d,0),相当于是取电容器截面各个方向向外延伸长度为d的一个观察面。
图 2‑6 旋转之后的坐标系及观察面模型
最后创建求解域(region),点击Create Region,在弹出的对话框Percentage Offset栏输入ratio1。创建region时,一般以已有实体模型在各个方向上的长度作为一个标准长度,各个方向上的Percentage就是以这个标准长度为基准,向各个方向延伸的比例。比如,+X方向填入100,就是Region在+X方向超出已有实体模型100%个标准长度,其余依此类推。此外,创建Region时还可以使用绝对值(Absolute Offset),此时填入的数据即为region伸出已有实体模型的长度。
(3)设置材料属性
右键单击模型树下的绝缘介质模型,选择Assign Material → Add Material,在Relative Permittivity后面输入10,即定义了一种相对介电常数为10的电介质材料。对于金属板,其材料可以直接采用默认的真空材料,或者将其设置为其他任何金属材料,这是因为,金属板为等势体,其相对介电常数对计算结果没有影响。计算域采用默认的真空即可。
(4)网格划分
右键单击模型树下的绝缘介质模型,选择Assign Mesh Operation → Inside Selection → Length Based,即在介质材料内部划分网格,将Maximum Length of Elements设置为d/2。采用相同的步骤,将Region的最大网格尺寸设置为a/2,将观察面的最大网格尺寸设置为d/2。对于金属板而言,因为本身就是等势体,网格优劣无关紧要(因为场梯度为零),将其网格尺寸设置为2b即可。
(5)施加载荷与边界条件
这里的载荷与边界条件相对比较简单,只需要对上下极板施加电压激励即可。右键单击模型树下的上极板模型,选择Assign Excitation → Voltage,在Value处输入1V。因为电容量与电压无关,这里施加一个单位电压即可。采用相同的操作,在下极板上添加0V电压。该模型中的边界为无穷远边界,可采用默认的边界条件。需要注意的是,在2D分析中,必须添加边界条件,3D中的无穷远边界可以采用默认边界。
(6)求解设置
右键单击工程树下的Analysis,选择Add Solution Setup,Maximum Number of Passes采用默认的10,即最大迭代步数为10步,Percent Error改为0.01,即收敛误差为0.01%,这个值设置的越小,求解精度越高。上述设置的意思是,在计算误差达到0.01%即认为计算收敛,停止计算;当迭代次数达到10步之后,即使没有达到设置的收敛条件,也会停止计算。设置的收敛误差越小,迭代的步数越多,网格越多,计算量也越大,计算机性能不足的同学可以设置为0.1。其他设置均采用默认值。为了计算电容量,还需要设置电容计算的设置。右键单击工程树下的Parameters,选择Assign → Matrix,在设置框内将Include下面的Voltage1和Voltage2均勾选,软件会自动计算这两个电压之间的电容参数。然后右键单击工程树下Analysis下面的Setup1,选择Apply Mesh Operations,此时软件会根据之前的预设网格参数划分网格。点击工具栏中的Validate,检查所有设置,确认无误后点击Analyze All开始计算。
2.3.3 电容的计算
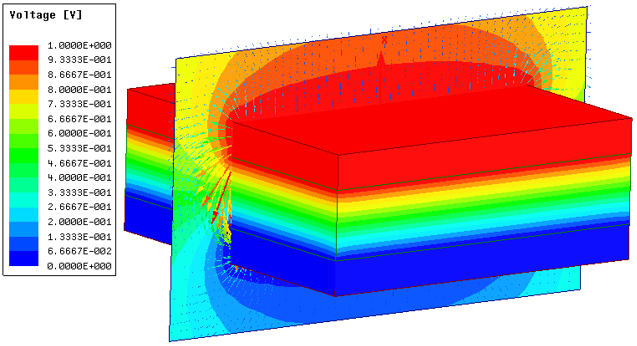
计算完成之后,我们可以通过简单的云图分布来对计算结果进行初步判断,以发现可能的问题。我们绘制观察面上电场E的矢量分布及观察面及极板、介质的表面电位分布,在模型树下选择观察面,单击右键选择Fields → E →E_vector,即完成观察面电场矢量的分布绘制。然后选中观察面及极板、电介质的表面(一种比较快捷的操作是,首先隐藏Region,然后键盘按一下F(选面快捷键),然后框选模型窗口的所有模型即完成所有面的选取),单击右键选择Fields → Voltage,即完成电位分布绘制。结果如图 2‑7所示,根据我们对平行板电容器的认识,判断计算结果是合理的。
图 2‑7 电位分布及电场矢量分布
在初步确定计算无误之后,就可以开始电容量的计算,电容量的计算方法有很多,下面逐一介绍。在求解设置中,我们已经设置了Matrix,这时软件自动计算电容,打开Solution Data → Matrix选项卡即可查看。电容矩阵包含4个元素,那是因为模型中共包含两个导体,每个导体与无穷远处的参考地之间有电容(为自电容),两个导体之间有互电容。这个电容矩阵中各个元素与前面式中矩阵各项是一一对应的,所以正负极板间的电容为4.76pF。
根据电容与能的关系 \(W=CU^2/2\) 这个公式,我们也可以通过计算系统储存的电场能来计算电容大小。在我们的计算中,取的电位差为1V,那么只需要计算2W即可得到电容值。具体操作如下:右键单击工作树下的Field Overlays → Calculator打开场计算器,点击Input栏Quantity → Energy(电场能密度),点击Input栏Geometry → Volume → AllObjects,点击Scalar栏的积分(∫),即计算整个空间的电场能;点击Input栏Number,在Value栏填入2,在确定后点击General栏乘号(*),点击Output栏Eval,计算得到2W的值,即为电容值。
此外,根据C=Q/U,我还可以通过计算导体上的电荷量来计算电容量。具体操作如下:右键单击工作树下的Field Overlays → Calculator打开场计算器,点击Input栏Quantity → QSurf(表面电荷密度),点击Input栏Geometry → Surface → Plate_up,点击Scalar栏的积分(∫),点击Output栏Eval,即计算出上极板的电荷量,即电容量。
2.3.4 求解域的选取
一般而言,电磁场是弥散在整个空间的,即Region应该是无穷大的,但是在仿真中我们不可能创建一个无穷的Region,而是采用一个有限的Region,配合合理的边界条件(气球边界)模拟无穷远。但是Region的大小仍然会对计算结果造成一定的影响,为了弄清楚Region大小对计算结果的影响,我们可以计算不同Region尺寸下的电容值的变化,来判断Region对计算结果的影响。
我们在建模时已经将Region的建模参数化了,这里只需进行参数化扫描即可。右键单击工作树下的Optimetrics,选择Add → Parametric,在Sweep Definitions选项卡下单击右侧的Add添加自变量,在新弹出对话框的Variable一栏选择ratio1,在下面Start栏、Stop栏和Step栏分别输入100、500和50,即考虑从1倍标准尺寸到5倍标准尺寸9种情况,然后单击Add>>完成自变量的添加。然后选择Calculations选项卡,单击Setup Calculations,在Category栏选择C(电容),在Quantity栏选择Matrix1.C(Voltage1,Voltage2),即计算两个极板互电容随ratio1的变化,最后单击Add Calculation。此时,我们还需要修改一下求解域的网格设置。之前的设置中,求解域网格设置为a/2,随着ratio1的变大求解域的网格将呈三次方增长,导致计算量太大,可以将求解域网格尺寸改为a/2*ratio1/100,即让其最大网格随着ratio1的增大而增加,保证计算效率。
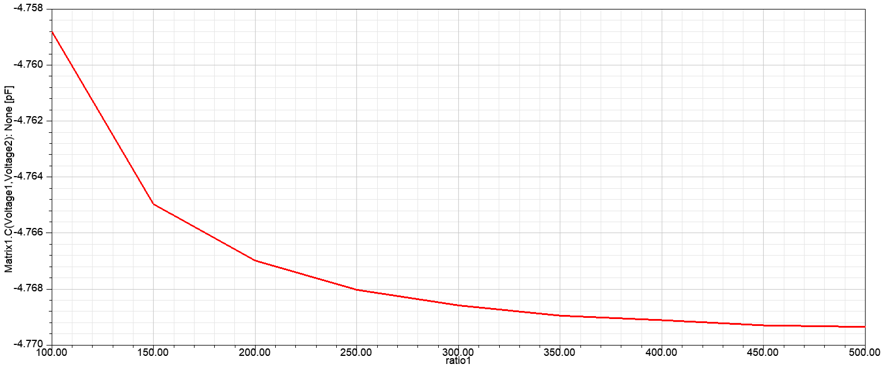
设置完成之后,右键单击工作树Optimetrics下的ParametricSetup1,选择Analyze开始计算。计算完成后,右键单击右键单击工作树Optimetrics下的ParametricSetup1,选择ViewAnalysisResult,得到电容与ratio1的关系曲线,如图2‑8所示。由计算结果可知,当ratio1达到400左右时,电容变化不再明显,即可认为Region的大小对电容的影响不大。事实上,由图2‑8可知,电容值约为4.77pF,即使ratio1取为100,误差也仅为0.23%。这说明,求解域对电容的计算结果有影响,但并不明显,这可能是因为平板电容的大部分电场能集中在介质区域,漏出来的电场线相对较少,或者说外部空间储存的电场能占比较小,因而弱化了求解域的影响。对于其他一些问题,如空芯线圈电感的计算问题,求解域的影响可能十分明显。
图 2‑8 电容值与Region的尺寸的关系
2.3.5模型对称性的使用
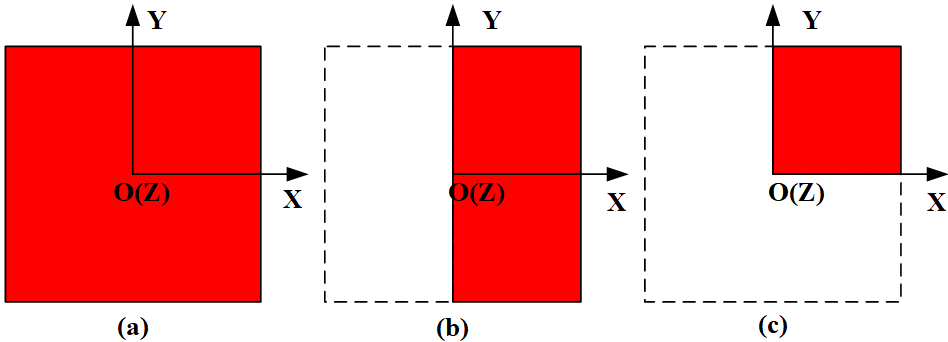
本案例中的模型不具备轴对称性或其中一维为无穷长等特点,所以难以用当作二维问题。但是我们知道,偏微分方程在确定边界条件之后解释唯一的(在暂态稳态中,还需要有初值)。在本案例的分析中,采用的是全模型+无穷远边界,那么有没有其他可以采用的边界条件呢?观察图2‑4可知,该平面电容器具有很明显的对称性,由电磁场的知识可知,YZ平面上的电场线均在该平面内。那么,在建模的时候,可以只建立一半的模型(如图2‑9(b)所示),并在YZ平面上施加相应对称边界条件(偶对称,场线平行)即可,由解的唯一性定理可知,这个1/2模型得到的解与全模型得到的解是完全相同的。此外,XZ也是一个对称面,场线也是与该平面平行的,那么就可以再利用一次对称性(偶对称,场线平行),只建立如图2‑9(c)所示的1/4模型,得到的解与全模型也是一样的。更进一步,XY平面位于电介质的中平面,其上的场线均与该平面垂直,那么就可以利用这一对称性(奇对称,场线垂直),建立1/8模型进行分析,这样就可以极大的提高分析效率。
图 2‑9 对称性及模型简化
下面介绍1/8模型的分析过程。单击工作树下的Maxwell3DDesign1,复制,然后单击工程树的顶端(工程名),粘贴,这样就把我们之前的分析模型复制到了一个新的任务Maxwell3DDesign2下,我们直接在里面对模型进行修改即可,无需重新建模。双击Maxwell3DDesign2,单击模型树下的Coordinate Systems →Global,即切换到全局坐标系下。
首先对仿真模型进行处理,删除观察面,选中上、下极板和电介质,单击右键选择Edit → Boolean→ Split,Split Plane选择XY,Keep fragments选择Positive side,即利用XY平面对所选模型进行分割,且只保留正向部分。重复上述操作,再分别利用YZ和XZ平面进行分割,即得到我们所需的1/8模型。此时需要注意的是,求解域的边界必须与对称面重合,我们还需要对Region的模型进行修改。双击模型树下的Region → CreateRegion,将三个方向负半轴的Padding Data全部改为0即可。最终得到的模型如图 2‑10所示。
图 2‑10 平板电容器1/8仿真模型
模型修改完成之后,还需要添加新的边界条件。在YZ和XZ平面上施加偶对称(Even,Flux Tangential),在XY平面上施加奇对称(Odd, Flux Normal)。然后右键单击工程树下Analysis下面的Setup1,选择Apply Mesh Operations,然后删除Optimetrics下的ParametricSetup1,就可以开始计算了。
计算完成之后可以在Solution Data下查看计算结果,计算得到的电容量为 \(C_{1/8}=2.35pF\) ,与先前计算的结果不一样,可以如下解释:全模型电容可以认为是8个1/8电容组成的,其中奇对称的电容器为串联关系,偶对称的电容器为并联关系,则总电容量 \(C=C_{1/8}*4/2=4.7pF\) ,与先前计算的结果一样。需要注意的是,在1/8模型中,我们只能对其中一个电极建模,在奇对称条件下,对一个电极施加1V的激励,另外一个电极的电位会默认为是-1V。因此,在利用能量法计算电容时,可以先计算1/8模型的能量 \(W_{1/8}\) ,然后利用 $2\times8W_{1/8}/U^2$ ,这里的电压应取为2V。此外,由于这种设定,采用1/8模型得到的介质中的电场强度也会与全模型不一样,但这并不影响电容的计算。关于1/2和1/4模型的分析,同学们可以自己尝试一下。
2.4 案例2——电容式角位移传感器
电容式传感器是将被测物理量或机械量转换为电容量的中转换装置,实际上就是一个参数可变的电容器。电容式传感器包含很多类,广泛的用于位移、角度、速度等方面的测量。
图 2‑11 角位移传感器3D简化模型
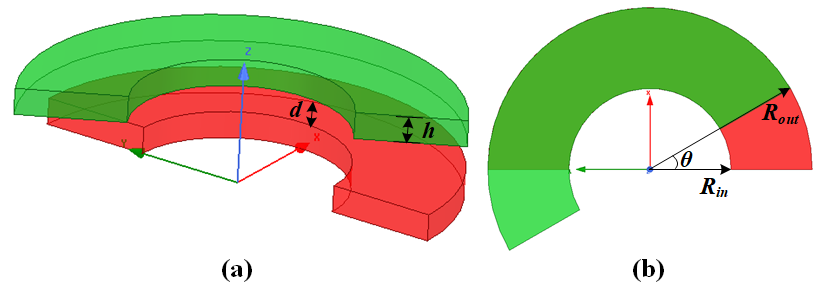
图2‑11所示为某型电容式角位移传感器模型,该角位移传感器主要由两个完全相同的半圆环形金属极板构成,极板内径 \(R_{in}\) =4mm,外径 \(R_{out}\) =8mm,厚度h=1mm,间距d=1mm,当两块点击之间的夹角θ发生变化时,两电极之间的电容也会发生变化,即可以通过电容量反应角位移。试分析θ在0°至180°的区间内,θ与电容量C之间的线性关系区间,同时计算θ与电容量C之间的比例系数。
2.4.1 本节知识点
辅助模型的建立
电容的计算
参数化扫描
2.4.2 分析模型的建立
(1)确定分析类型
分析这个问题可知,模型不规则,不具备旋转对称性或无穷长的特点,因此可以确定为是一个3D静电场问题。点击Insert Maxwell 3D Design图标,新建一个3D仿真任务,然后点击工具栏Maxwell 3D → Solution Type,弹出新的对话框中,求解器选择Electrostatic。
(2)建立分析模型
在建模之前,为了实现建模的参数化,需要首先定义参数变量,具体操作参考案例1。夹角θ是需要扫描的参数,初始定义可以随便给一个值。
首先创建下极板。下极板是一个半圆环,创建的方法很多,推荐以下两种。第一种,先创建厚度为h、半径分别为 \(R_{in}\) 和 \(R_{out}\) 的两个圆柱,然后利用Edit → Boolean →Subtract得到一个圆环,再利用Edit → Boolean →Split将圆环分割,得到圆环;第二种,首先创建一个圆环的截面(矩形,宽 \(R_{out}-R_{in}\) ,高h),然后利用Edit → Sweep → Around Axis,将截面绕坐标轴旋转180°得到半圆环。
然后创建上极板。上基本可以直接通过下极板的复制得到,即利用Edit → Duplicate → Along Line将下极板沿直线复制即可。然后还需要利用Edit → Arrange → Rotate将上极板进行选装,并将旋转角设置为之前预设的角度变量θ。
由于两极板之间的区域场梯度较大,需要相对密集的网格,因而可以专门在两极板之间创建一个辅助模型,用于两极板之间网格的细分,同时又不增加其他区域的网格数量,兼顾计算精度与效率。在两极板之间的区域创建一个内径 \(R_{in}\) 、外径 \(R_{out}\) 、高度为d的圆环即可。
最后创建Region,将极板上下两个方向的比例设置为300,其他方向设置为100。得到的仿真模型如图2‑12所示,具体操作参见案例视频。
图 2‑12 角位移传感器仿真分析模型
(3)设置材料属性
因为电极属于等势体,其材料对计算无影响,可采用默认材料;Region和辅助模型区域也采用默认的Vacuum。
(4)网格划分
因为电极属于等势体,网格可以不用设置;两电极之间的区域为场梯度较大的区域,网格需要设置的较密,最大尺寸设置为d;Region的最大网格设置为 \(R_{in}\) 。具体操作参考案例1。
(5)施加载荷与边界条件
载荷比较简单,分别将上、下极板电位设置为0V和1V即可。对于边界条件,由于是3D仿真,且没有采用任何对称条件,可采用默认边界。
(6)求解设置
将计算精度设置为0.1%,同时在Parameters里设置电容矩阵,具体操作参考案例1。此外,还需要设置参数化扫描分析,以计算电容与角位移的依赖关系。在Optimetrics里设置关于角位移θ的参数化分析,取值范围为0:10:180,在Setup Sweep Analysis窗口Calculations选项卡下设置计算量Matrix1.C(Voltage1, Voltage2),具体操作参考案例1。设置完成后点击Validate检查设置,确认无误后开始计算。
2.4.3 计算结果的处理与分析
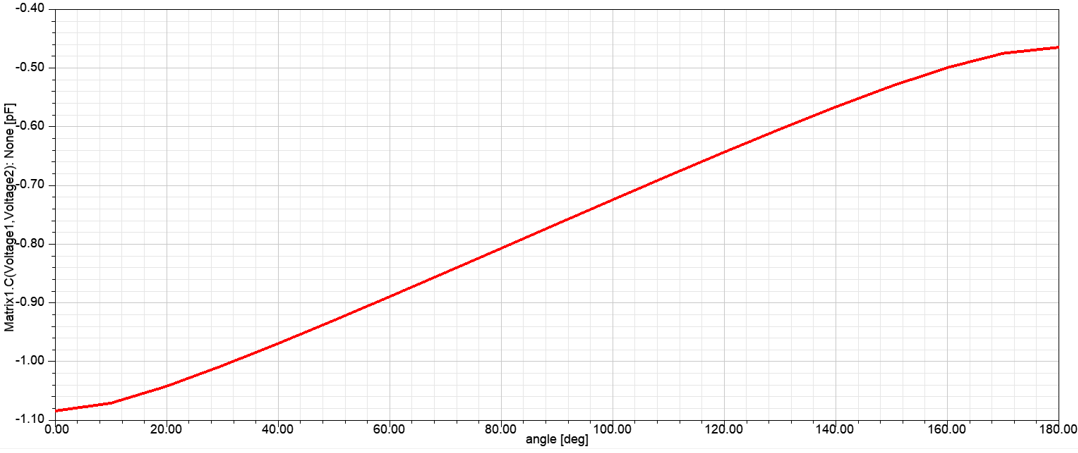
计算完成之后,可以右键单击工作树Optimetrics下的ParametricSetup1,选择ViewAnalysisResult,得到电容与角位移的关系曲线,如图2‑13所示。由计算结果可知,在很大范围内( 20°至160° ),电容量与角位移都呈现很好的线性关系,且比例系数约为 $3.9×10^{-15}F/degree$ 。
为了更好的分析电容量与角位移的关系,还可以将计算结果数据导出,然后利用MATLAB进行相关数据的分析。
图 2‑13 电容量与角位移的关系曲线
更多案例请在参考资料[3]和参考资料[4]中查阅。
本文章使用limfx的vsocde插件快速发布