密度泛函理论基本

回到主页

一些定义

波函数(wave function)

为复数函数，表示在空间位置和时间找到所描述粒子的概率幅，表示在相应时空位置找到该粒子的概率密度。因此，以一维空间中运动的粒子为例，粒子在 的概率为

P_{a \leq x \leq b}=\int_{a}^{b}|\Psi(x, t)|^{2} \mathrm{~d} x

显然，粒子在全空间上出现的概率为1（归一性），即

\int_{-\infty}^{\infty}|\Psi(x, t)|^{2} \mathrm{~d} x=1

下图是一维空间粒子波函数的两个示例 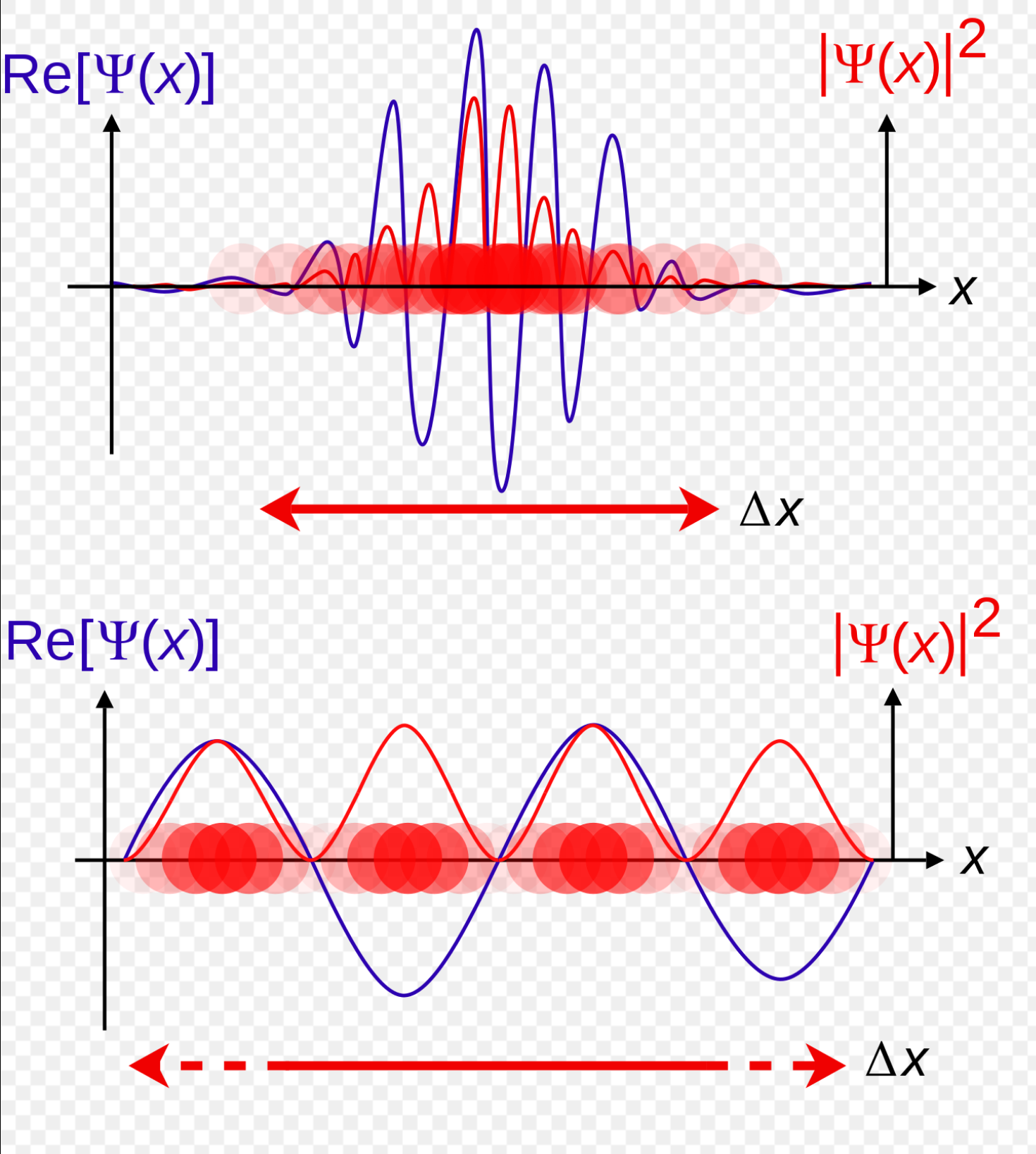波函数实部（紫色），概率密度（红色）

算子（Operator）

比如微分算子

量子力学算符

量子力学可观测量都可由算符表示，比如动能算符

基态（Ground state）

能量最低，体系最稳定的状态

固体中的多体问题

求解以下多体薛定谔方程，即可得到体系基态

\widehat{\boldsymbol{H}} \boldsymbol{\psi}\left(\left\{r_{i}\right\},\left\{R_{I}\right\}\right)=\boldsymbol{E} \boldsymbol{\psi}\left(\left\{r_{i}\right\},\left\{R_{I}\right\}\right)

其中，表示电子的位置，表示原子核的位置，为带电粒子库伦能以及动能算符的总和。 求解这样的问题是复杂的，为此给出以下近似。

Born Oppenheimer approximation（多体多电子）

原子核质量远大于电子质量。因此，电子运动比原子核快得多，可以将原子核运动和电子运动分离处理，先固定原子核，从而对波函数进行解耦，即

\psi\left(\left\{r_{i}\right\},\left\{R_{l}\right\}\right) \rightarrow \psi_{N}\left(\left\{R_{l}\right\}\right) * \psi_{e}\left(\left\{r_{i}\right\}\right)

于是，多体薛定谔方程可变为多电子薛定谔方程，即

\widehat{H} \psi\left(\boldsymbol{r}_{\mathbf{1}}, \boldsymbol{r}_{2}, \boldsymbol{r}_{3} \ldots \boldsymbol{r}_{N}\right)=E \psi\left(\boldsymbol{r}_{1}, \boldsymbol{r}_{2}, \boldsymbol{r}_{3} \ldots \boldsymbol{r}_{N}\right)

电子哈密顿量为

    \widehat{\boldsymbol{H}}=-\frac{\hbar^{2}}{2 m_{e}} \sum_{i}^{N_{e}} \nabla_{i}^{2}+\sum_{i}^{N_{e}} V_{e x t}\left(r_{i}\right)+\sum_{i=1}^{N_{e}} \sum_{j>1} U\left(r_{i}, r_{j}\right)

其中，第一项表示电子动能，第二项表示电子和原子核相互作用能，第三项为电子和电子的相互排斥能。 即使暂时不考虑原子核，求解上述薛定谔方程仍是困难的，方程的维度是。

密度泛函理论 (波函数 电子密度)

电子密度定义

    n(\boldsymbol{r})=\psi^{*}\left(\boldsymbol{r}_{1}, \boldsymbol{r}_{2} \ldots r_{N}\right) \psi\left(r_{1}, r_{2} \ldots r_{N}\right)

更进一步，对于多电子问题，可以认为某一电子是在其他电子产生的总电场中运动，那么多电子波函数可认为是

    \psi\left(r_{1}, r_{2}, r_{3} \ldots r_{N}\right)=\psi\left(r_{1}\right) * \psi_{2}\left(r_{2}\right) * \psi_{3}\left(r_{3}\right) * \cdots * \psi_{N}\left(r_{N}\right)

对应的电子密度可写为

    n(\boldsymbol{r})=2 \sum_i^{N_e} \psi_{i}^{*}(r) \psi_{i}(r)

从而多电子问题可以转化为单电子问题。

密度泛函理论基本定理

  1. 定理一 基态能量是电子密度的泛函，即。
  2. 最低能量对应的电子密度即为基态电子密度，即 为此，我们需要了解能量泛函的具体形式，如下
    E\left[\left\{\psi_{i}\right\}\right]=E_{\text {known }}\left[\left\{\psi_{i}\right\}\right]+E_{X C}\left[\left\{\psi_{i}\right\}\right]

其中，已知表达式的泛函包括电子动能项、电子原子核相互作用项、电子电子相互作用项以及原子核原子核相互作用项，即

    \begin{aligned}
&E_{\text {known }}\left[\left\{\psi_{i}\right\}\right]=-\frac{\hbar}{m_{e}} \sum_{i} \int \psi_{i}^{*} \nabla^{2} \psi_{i} d^{3} r+\int V(r) n(r) d^{3} r+\frac{e^{2}}{2} \iint \frac{n(r) n\left(r^{\prime}\right)}{r-r^{\prime}} d^{3} r d^{3} r^{\prime}+E_{i o n}
\end{aligned}

不存在解析表达式的能量泛函为交换关联泛函,该项包含所有的量子相互作用，常用的两种近似为LDA(Local density approximation) 和 GGA (Generalized gradient approximation)。

Kohn Sham Scheme

求解单电子波函数方程

\left[-\frac{\hbar}{2 m} \nabla^{2}+V(\boldsymbol{r})+V_{\mathrm{H}}(\mathbf{r})+\mathrm{V}_{\mathrm{XC}}(\mathbf{r})\right] \psi_{i}(\boldsymbol{r})=\epsilon_{i}(\boldsymbol{r}) \psi_{i}

哈密顿量中第一项为电子动能，第二项为电子原子核相互作用，第三项为电子与具有电子密度的电子气相互作用能，第四项为交换关联泛函。 基本算法流程为

  1. 给定初始电子密度；
  2. 求解单电子薛定谔方程得到波函数；
  3. 根据单电子波函数得到电子密度；
  4. 新的电子密度和上一步电子密度比较，判断是否收敛。

晶体和平面波

本文章使用limfx的vscode插件快速发布