VASP基本操作

回到主页

by 之航

一. 基本概念

Background-密度泛函理论[1]

密度泛函理论 (Density Functional Theory): 密度泛函理论（DFT） 的许多常用泛函均包含由实验数据拟合而来的参数。但在解决分子的电子结构问题时也常将密度泛函理论被当做第一原理方法。密度泛函理论使用电子密度而不是波函数来表述体系能量。在DFT计算中，哈密顿量的一项，交换-相关泛函，采用近似形式。

封面

  • 不含时薛定谔方程   其中是不含时波函数，是能量，即能量的本征值。 薛定谔方程

三维空间里，处于位势的单独粒子，其不含时薛定谔方程的表示

-\frac{\hbar}{2m}\nabla^2\psi(r)+V(r)\psi(r) = E\psi(r)
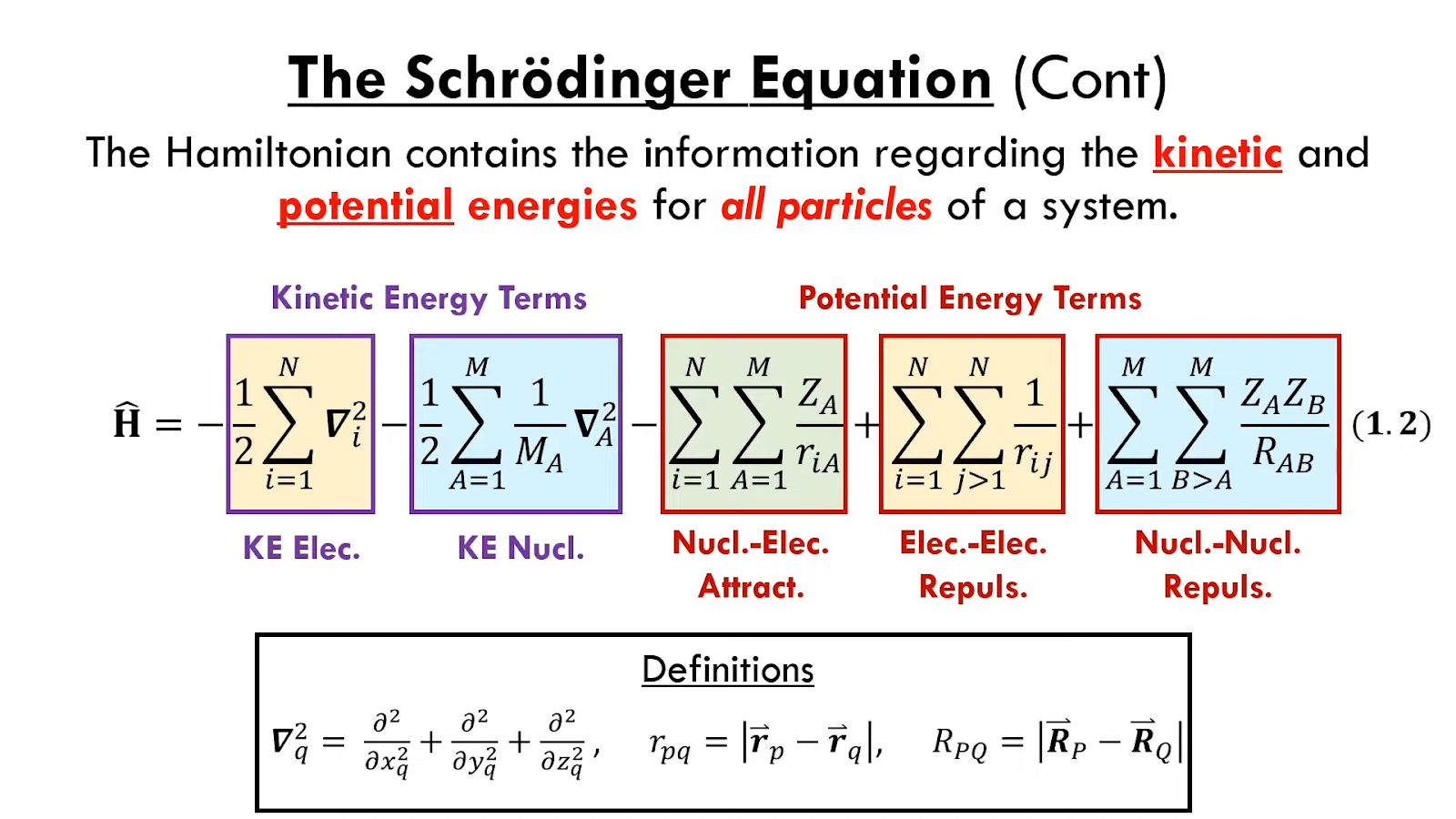
  • 量子力学中，哈密顿算符()是一个可观测量，对应系统的总能量。 哈密顿算符
  • 玻恩–奥本海默近似 玻恩–奥本海默近似 玻恩–奥本海默近似

将原子核坐标与电子坐标的近似变量分离，求解整个体系的波函数的复杂过程分解为求解电子波函数和求解原子核波函数两个相对简单得多的过程。在玻恩－奥本海默近似下，体系波函数可以被写为电子波函数与原子核波函数的乘积。

\Psi_{total} = \chi_{electronic}\times\phi_{unclear}

基态

波函数

每个是薛定谔方程本身的解，它们的乘积至少应该近似解。这种组合单个电子的波函数的简单方法被称为Hartree product。

  • 电子密度 电子密度

In quantum chemistry, electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised N-electron wavefunction which itself depends upon 4N variables 3N spatial and N spin coordinates). Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.

密度泛函理论

Hohenberg-Kohn 定理一：薛定谔方程中基态能量是电子密度的函数； Hohenberg-Kohn 定理二：能量最低的电子密度是薛定谔方程的正解。

函数

KH理论

交换关联势

交换关联函定义：交换关联函（exchange-correlation functional）是KS方程里除了动能项、势能项的第三项，其他所有的相互作用都包含在这一项中。

DFT12

DFT13

求解

LDA

GGA

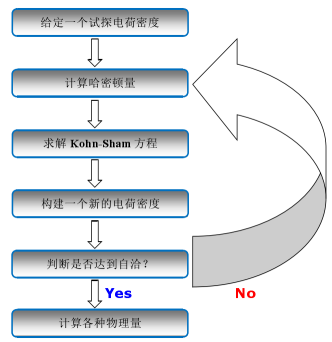
1. VASP计算流程

  VASP用来计算多体薛定谔方程的近似解，在密度泛函理论 (DFT) 内求解 Kohn-Sham (KS) 方程，或在 Hartree-Fock (HF) 近似内求解薛定谔方程。

  1. 第一性原理
    • 基于密度泛函的从头算：通过电子密度作为基本变量，通过求解 Kohn-Sham 方程，迭代得到体系的电子密度，然后求体系的基态性质；同时考虑了电子间的交换关联作用。
    • 基于Hartree-Fock自洽计算的从头算：通过自洽求解Hartree-Fock方程，获得体系的波函数，求基态性质。
  2. 泛函
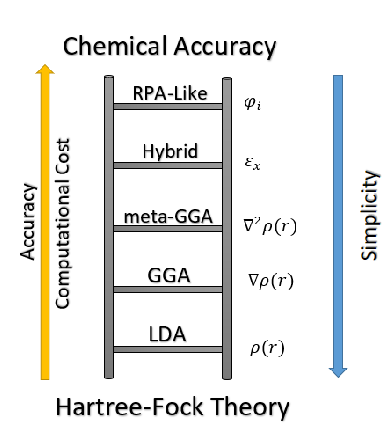
  • 泛函是指交换关联泛函，包括LDA、GGA、杂化泛函等。LDA为局域密度近似，在空间使用某点均匀的电子气作为交换关联泛函的唯一变量，局域密度近似的交换相关泛函可以写作：
E_{xc}^{LDA}[\rho] = \int\rho(r)\varepsilon_{XC}(\rho)\mathrm{d}r

为电子密度， 为交换相关能量密度。

  • GGA为广义梯度近似，不仅将电子密度作为交换关联泛函的变量，同时也考虑了密度的梯度作为变量，包括PBE、PW、RPBE等方案。
  1. 赝势
  2. 收敛测试
  3. 磁性
  4. 几何优化
flowchart LR
    id1(结构优化)
    id2(静态自洽)
    id3(非自洽计算)
    id1-->id2-->id3
  1. 结构优化（弛豫） 结构优化指对整个输入的坐标系进行调整，得到一个相对稳定的结构

2. 输入文件

  • INCAR
  • POSCAR
  • POTCAR
  • KPOINTS

3. 输出文件

  • OUTCAR
  • DOSCAR
  • CHGCAR

二. 收敛性测试

三. 结构优化（结构弛豫）

四. 吸附能计算

五. 解离能计算

六. 态密度计算

七. 差分密度电荷计算

八. LUMO、HUMO计算

九. Bader分析

十. Practices

Reference

  1. Density Functional Theory: A Practical Introduction. ↩︎

本文章使用limfx的vscode插件快速发布