复合材料力学涉猎——复合材料层合板的刚度和强度

• 1 绪论

• 2 层合板的表示方法

• 3 一般层合板的弹性分析

  • 3.1 假设

  • 3.2 层合板的应力和应变关系

  • 3.3 层合板的合力及合力矩

• 4 对称层合板的刚度特性

  • 4.1 单层层合板的刚度

  • 4.2 正交铺设对称层合板的刚度

  • 4.3 斜交铺设对称层合板

• 5 两种非对称层合板的刚度

  • 5.1 规则非对称正交铺设层合板

  • 5.2 规则反对称层合板

• 6 平行移轴定理

• 7 湿热效应对层合板刚度影响

  • 7.1 单层的湿热变形

  • 7.2 含湿热应变的单层应力应变关系

  • 7.3 含湿热效应的层合板内力-应变关系

• 8 层合板的强度

  • 8.1 最先一层失效强度

  • 8.2 极限强度

  • 8.3 湿热效应对层合板强度的影响

    • 8.3.1 层合板的残余应变和残余应力

    • 8.3.2 考虑残余应力的层合板强度计算

• 9 总结

1 绪论

层合板是由两层或者两层以上的单层板粘合在一起成为整体的结构元件。复合材料层合板的平面尺寸有一个到两个方向的尺寸比厚度大很多。符合材料层合板被看作基本的平板。

基本假设有：层合板为连续、均匀、正交各向异性的单层构成的一种连续性材料；各单层之间是完全紧密黏结的，材料特性为线弹性，结构变形为小变形。

涉及到的知识：材料力学、弹性力学、高等数学、线性代数、复合材料单层的刚度和强度。

2 层合板的表示方法

如图所示为复合材料层合板的表示方法：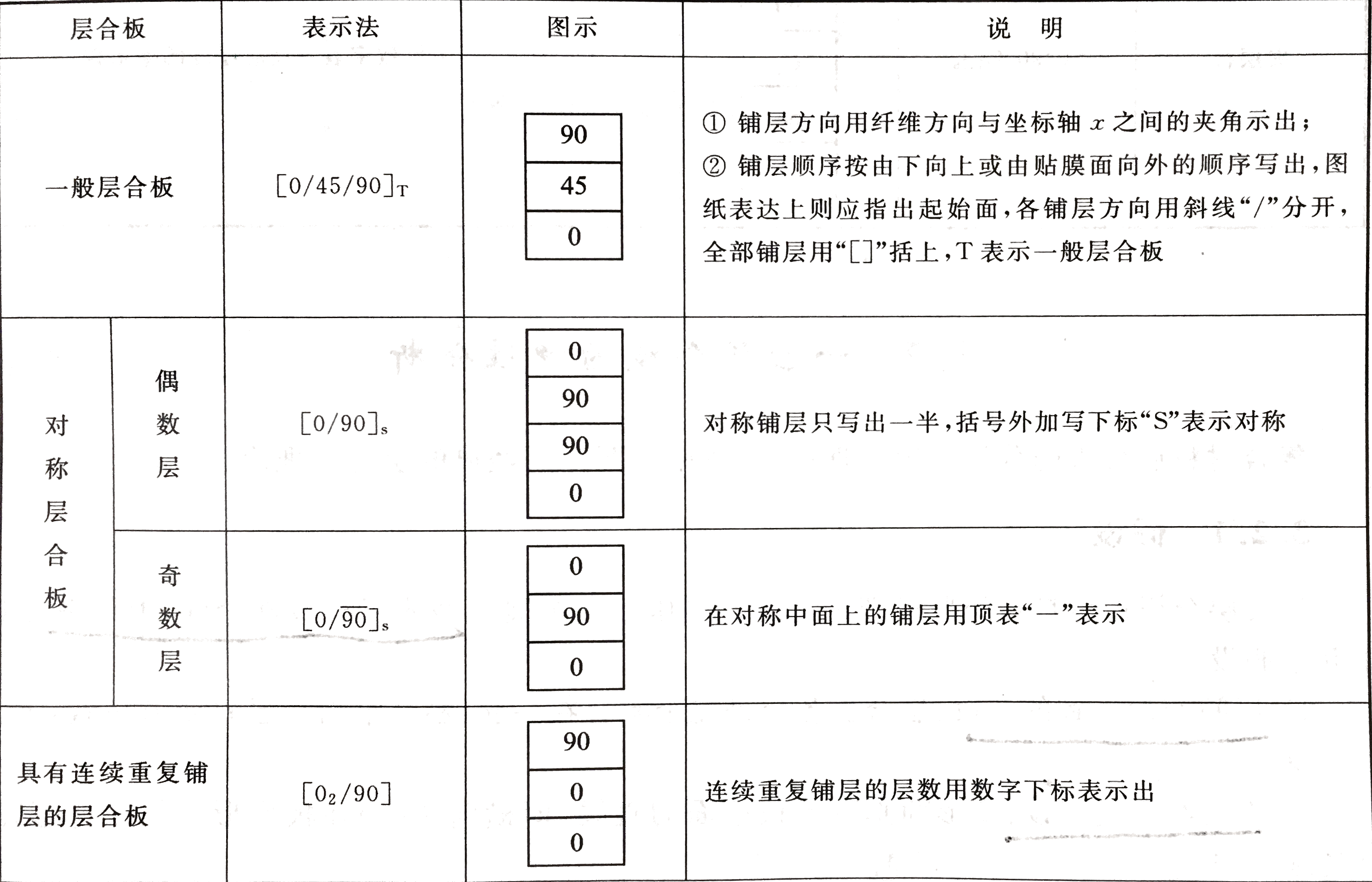


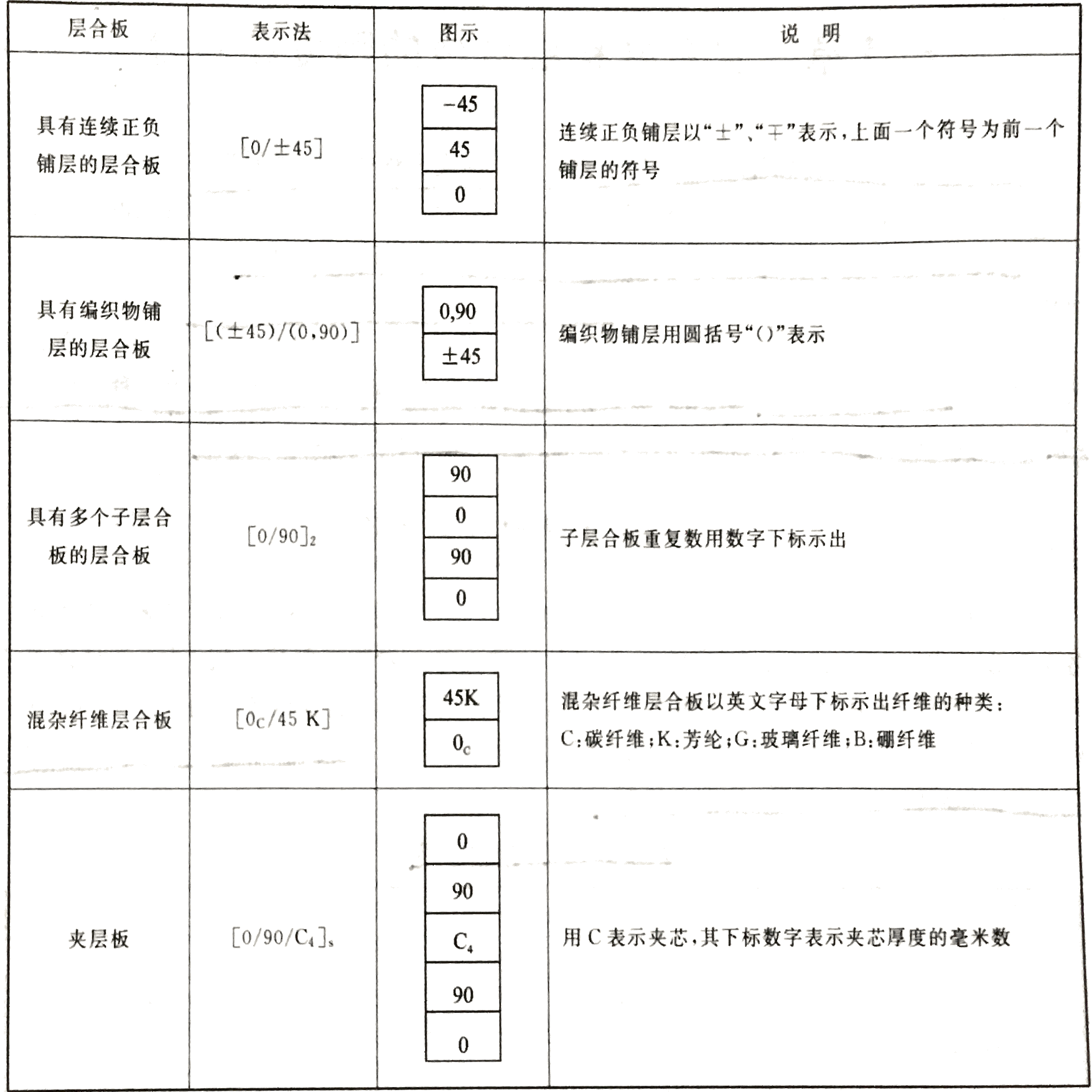
表中各单层的材料性能与厚度均相同。以后除非特殊说明，均按此限制。

3 一般层合板的弹性分析

这里介绍经典的层合板理论。

3.1 假设

1. 层间变形一致的假设：层合板各层是完全黏合在一起（粘合牢固），层间变形一致，无相对位移。

2. 直法线不变假设：变形前垂直于板中面的直线（即横向法线）在板变形后仍保持垂直，即${\gamma }_{xz}={\gamma }_{yz}=0$。且长度不变，即${ϵ}_z=0$。

3. ${\sigma }_z=0$假设：在厚度方向上的正应力与其它应力相比很小，可以忽略不计。

4. 平面应力假设：各单层板处于平面应力状态。

3.2 层合板的应力和应变关系

如图所示，考虑一个总厚度为$h$的$N$层正交异性板，取中面为$xy$坐标面，$z$轴垂直板中面，z轴取中面向下为正，第$k$层位于厚度方向$z=z_k$和$z=z_{k+1}$之间。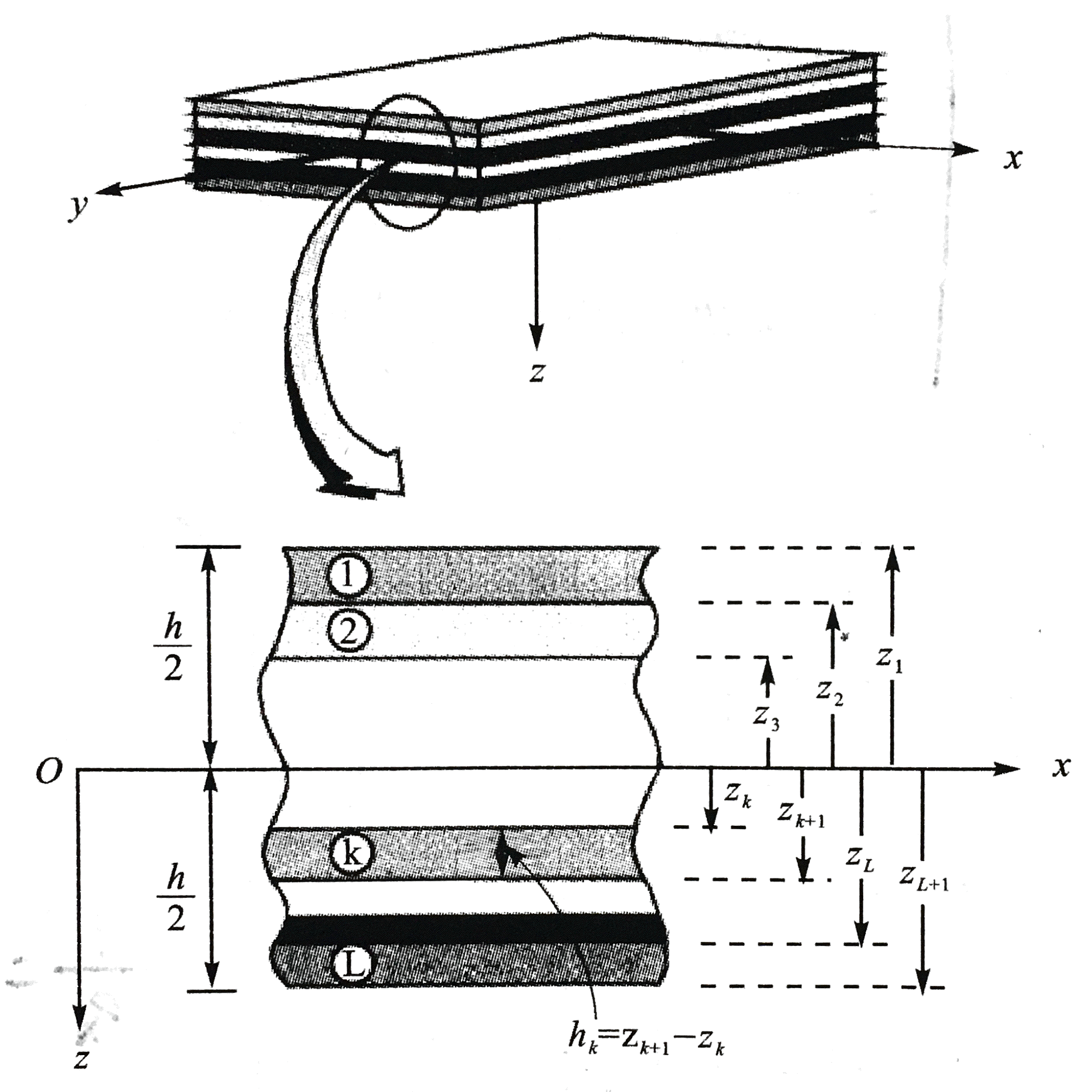

设层合板上任意一点$(x,y,z)$移动到变形后层合板$(x+u,y+v,z+w)$处，其中位移可表示为：

$$\begin{array}{c}u=u(x,y,z)\\ v=v(x,y,z)\\ w=w(x,y,z)\end{array}\}$$

根据基本假设2，以及弹性力学几何方程：

$$\begin{array}{c}{ϵ}_z=\frac{\partial w}{\partial z}=0\\ {\gamma }_{xz}=\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}=0\\ {\gamma }_{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}=0\end{array}\}$$

由上式第一式得：

$$w=w_0(x,y)$$

由第二式得：

$$\frac{\partial u}{\partial z}=-\frac{\partial w}{\partial x}$$

对$z$积分得：

$$u=-\int \frac{\partial w}{\partial x}\mathrm{d}z+C_1(x,y)$$

代入$w=w_0(x,y)$得：

$$u=-z\frac{\partial w_0}{\partial x}+C_1(x,y)+C_2(x,y)$$

令$C_1(x,y)+C_2(x,y)=u_0(x,y)$得：

$$u=u_0(x,y)-z\frac{\partial w_0}{\partial x}$$

同理可得$v$，综合得：

$$\begin{array}{c}u(x,y,z)=u_0(x,y)-z\frac{\partial w_0}{\partial x}\\ v(x,y,z)=v_0(x,y)-z\frac{\partial w_0}{\partial y}\\ w(x,y,z)=w_0(x,y)\end{array}\}\text{\hspace{1em}(3.2.1)}$$

观察上式，当$z=0$时，$u=u_0,v=v_0,w=w_0$。故称这三个量为中面位移分量。三维位移场被简化为一种仅考虑中面变形面的位移场。一旦中面位移$(u_0.v_0,w_0)$已知，对任意三维连续点的位移$(x,y,z)$可确定。同时也可以利用几何方程确定应变。

$$\begin{array}{c}{ϵ}_x=\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2}\\ {ϵ}_y=\frac{\partial u_0}{\partial y}-z\frac{{\partial }^2{w}_0}{\partial y^2}\\ {\gamma }_{xy}=\frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}-2z\frac{{\partial }^2{w}_0}{\partial x\partial y}\end{array}\}$$

可简写为：

$$\mathbf{ϵ}={\mathbf{ϵ}}^{(0)}+z\mathbf{\kappa }\text{\hspace{1em}(3.2.2)}$$

其中：

$$\mathbf{ϵ}=\left[\begin{array}{c}{ϵ}_x\\ {ϵ}_y\\ {\gamma }_{xy}\end{array}\right],{\mathbf{ϵ}}^{(0)}=\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\end{array}\right]=\left[\begin{array}{c}\frac{\partial u_0}{\partial x}\\ \frac{\partial v_0}{\partial y}\\ \frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}\end{array}\right],\mathbf{\kappa }=\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right]=\left[\begin{array}{c}-\frac{{\partial }^2{w}_0}{\partial x^2}\\ -\frac{{\partial }^2{w}_0}{\partial y^2}\\ -2\frac{{\partial }^2{w}_0}{\partial x\partial y}\end{array}\right]$$

称$({ϵ}_x^{(0)},{ϵ}_y^{(0)},{\gamma }_{xy}^{(0)})$为中面应变，$({\kappa }_x,{\kappa }_y,{\kappa }_{xy})$为中面曲率，${\kappa }_{xy}$为中面的扭曲率。

代入第$k$层的偏轴单层板应力-应变关系式${\mathbf{\sigma }}^{(k)}={\overline{\mathbf{Q}}}^{(k)}{\mathbf{ϵ}}^{(k)}$得：

$${\mathbf{\sigma }}^{(k)}={\overline{\mathbf{Q}}}^{(k)}({\mathbf{ϵ}}^{(0)}+z\mathbf{\kappa })\text{\hspace{1em}(3.2.3)}$$

通过$(3.2.2)$和$(3.2.3)$可以看出：应变是沿厚度线性变化的。而由于每块单层的模量矩阵${\overline{\mathbf{Q}}}^{(k)}$不同，应力一般不是沿厚度线性变化的。

3.3 层合板的合力及合力矩

由于层合板的应力沿厚度方向非线性变化，所以我们转而研究内力合力与应变的关系。

如图所示，作用于层合板上的合力${\mathbf{N}}_{\mathbf{x}},{\mathbf{N}}_{\mathbf{y}},{\mathbf{N}}_{\mathbf{x}\mathbf{y}}$与合力矩${\mathbf{M}}_{\mathbf{x}},{\mathbf{M}}_{\mathbf{y}},{\mathbf{M}}_{\mathbf{x}\mathbf{y}}$（都是指单位长度上的力和力矩）：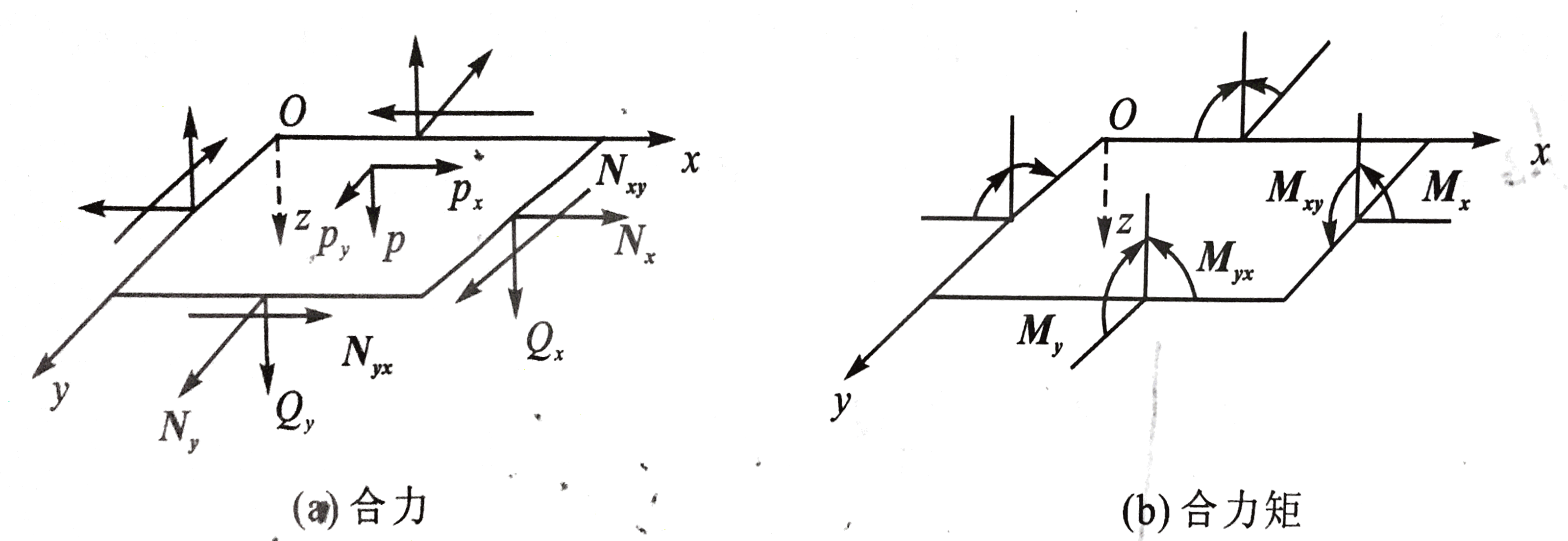

则有：

$$\begin{array}{c}{N}_x={\int }_{-h/2}^{h/2}{\sigma }_x\mathrm{d}z={\sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}{\sigma }_x^{(k)}\mathrm{d}z\\ N_y={\int }_{-h/2}^{h/2}{\sigma }_y\mathrm{d}z={\sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}{\sigma }_y^{(k)}\mathrm{d}z\\ N_{xy}={\int }_{-h/2}^{h/2}{\tau }_{xy}\mathrm{d}z={\sum }_{k=1}^N{\int }_{z_k}^{z_{k+1}}{\tau }_{xy}^{(k)}\mathrm{d}z\end{array}\}$$

以及

$$\begin{array}{c}{M}_x={\int }_{-h/2}^{h/2}{\sigma }_{x}z\mathrm{d}z={\sum }_{k=1}^M{\int }_{z_k}^{z_{k+1}}{\sigma }_x^{(k)}z\mathrm{d}z\\ M_y={\int }_{-h/2}^{h/2}{\sigma }_{y}z\mathrm{d}z={\sum }_{k=1}^M{\int }_{z_k}^{z_{k+1}}{\sigma }_y^{(k)}z\mathrm{d}z\\ M_{xy}={\int }_{-h/2}^{h/2}{\tau }_{xy}z\mathrm{d}z={\sum }_{k=1}^M{\int }_{z_k}^{z_{k+1}}{\tau }_{xy}^{(k)}z\mathrm{d}z\end{array}\}$$

代入$(3.2.3)$。由于中变应变${\mathbf{ϵ}}^{(0)}$和中面曲率$\mathbf{\kappa }$不随$z$变化，模量矩阵${\overline{\mathbf{Q}}}^{(k)}$在每层是不变的，则可以将前两者提到求和号外面；后者提到积分号外面，求和号里面。即：

$$\begin{gathered} \mathbf{N}=(\sum _{k=1}^N{\overline{\mathbf{Q}}}^{(k)}{\int }_{z_k}^{z_{k+1}}\mathrm{d}z){\mathbf{ϵ}}^{(0)}+(\sum _{k=1}^N{\overline{\mathbf{Q}}}^{(k)}{\int }_{z_k}^{z_{k+1}}z\mathrm{d}z)\mathbf{\kappa } \\ \mathbf{M}=(\sum _{k=1}^N{\overline{\mathbf{Q}}}^{(k)}{\int }_{z_k}^{z_{k+1}}z\mathrm{d}z){\mathbf{ϵ}}^{(0)}+(\sum _{k=1}^N{\overline{\mathbf{Q}}}^{(k)}{\int }_{z_k}^{z_{k+1}}{z}^2\mathrm{d}z)\mathbf{\kappa } \end{gathered}$$

计算积分得：

$$\begin{array}{c}\mathbf{N}=\mathbf{A}{\mathbf{ϵ}}^{(0)}+\mathbf{B}\mathbf{\kappa }\\ \mathbf{M}=\mathbf{B}{\mathbf{ϵ}}^{(0)}+\mathbf{D}\mathbf{\kappa }\end{array}\}\text{\hspace{1em}(3.3.1)}$$

其中$\mathbf{A}$、$\mathbf{B}$和$\mathbf{D}$分别被称为面内刚度矩阵、耦合刚度矩阵和刚度柔度矩阵：

$$\begin{array}{c}{A}_{ij}={\sum }_{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}-z_k)\\ B_{ij}=\frac{1}{2}{\sum }_{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}^2-z_k^2)\\ D_{ij}=\frac{1}{3}{\sum }_{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}^3-z_k^3)\end{array}\}\text{\hspace{1em}(3.3.2)}$$

可写成矩阵形式：

$$\left[\begin{array}{c}\mathbf{N}\\ \mathbf{M}\end{array}\right]=\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ \mathbf{B}& \mathbf{D}\end{array}\right]\left[\begin{array}{c}{\mathbf{ϵ}}^{(0)}\\ \mathbf{\kappa }\end{array}\right]$$

展开写即为：

$$\left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\\ M_x\\ M_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{cccccc}{A}_{11}& A_{12}& A_{16}& B_{11}& B_{12}& B_{16}\\ A_{21}& A_{22}& A_{26}& B_{21}& B_{22}& B_{26}\\ A_{61}& A_{62}& A_{66}& B_{61}& B_{62}& B_{66}\\ B_{11}& B_{12}& B_{16}& D_{11}& D_{12}& D_{16}\\ B_{21}& B_{22}& B_{26}& D_{21}& D_{22}& D_{26}\\ B_{61}& B_{62}& B_{66}& D_{61}& D_{62}& D_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\\ {\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right]\text{\hspace{1em}(3.3.3)}$$

因为${\overline{\mathbf{Q}}}^{(k)}$为对称矩阵，则$\mathbf{A}$、$\mathbf{B}$、$\mathbf{D}$以及它们组合起来的刚度矩阵均为对称矩阵。

可以看出一般情况下，层合板面面内内力（轴力和剪力）会引起弯曲变形（弯曲和扭转）；而弯曲内力（弯矩和扭矩）会一起面内变形（拉伸和剪切）。轴力会引起剪切，剪力也会引起拉伸；弯矩会引起扭转，扭矩会引起弯曲。其关系耦合可表示为如图所示：

拉、剪、弯和扭表示对应的四种力或变形。其相互之间的连线表示有耦合关系，若有叉则无耦合关系。126对应刚度矩阵中的系数下标，即拉和弯对应12（1为x方向，2为y方向），剪和扭对应6。（刚度矩阵系数下标中的第一个表示力，第二个表示变形）。$A$对应刚度矩阵中的系数$A_{ij}$，表示其为拉-剪耦合。$D$对应刚度矩阵中的系数$D_{ij}$，表示其为弯-扭耦合。$B$对应刚度矩阵中的系数$B_{ij}$，表示其为拉（剪）-弯（扭）耦合。由于刚度矩阵所有系数都不为零，所以连线之间没有叉，四个方向相互耦合。

求刚度矩阵逆矩阵得：

$$\left[\begin{array}{c}{\mathbf{ϵ}}^{(0)}\\ \mathbf{\kappa }\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}}^{\prime }& {\mathbf{B}}^{\prime }\\ {\mathbf{B}}^{\prime }& {\mathbf{D}}^{\prime }\end{array}\right]\left[\begin{array}{c}\mathbf{N}\\ \mathbf{M}\end{array}\right]$$

其中${\mathbf{A}}^{\prime }$、${\mathbf{B}}^{\prime }$和${\mathbf{D}}^{\prime }$分别被称为面内柔度矩阵、耦合柔度矩阵和弯曲柔度矩阵：

$$\begin{gathered} {\mathbf{A}}^{\prime }={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{B}(\mathbf{D}-\mathbf{B}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1}\mathbf{B}{\mathbf{A}}^{-1} \\ {\mathbf{B}}^{\prime }=-{\mathbf{A}}^{-1}\mathbf{B}(\mathbf{D}-\mathbf{B}{\mathbf{A}}^{-1}\mathbf{B}{)}^{-1} \\ \mathbf{D}=(\mathbf{D}-{\mathbf{B}\mathbf{A}}^{-1}\mathbf{B}{)}^{-1} \end{gathered}$$

为使层合板刚度矩阵与单层模量矩阵相比较，将刚度矩阵、力和应变做如下正则化处理：

$$\begin{array}{c}{\mathbf{A}}^{\ast }=\frac{1}{h}\mathbf{A},{\mathbf{B}}^{\ast }=\frac{2}{h^2}\mathbf{B},{\mathbf{D}}^{\ast }=\frac{12}{h^3}\mathbf{D}\\ {\mathbf{N}}^{\ast }=\frac{1}{h}\mathbf{N},{\mathbf{M}}^{\ast }=\frac{6}{h^2}\mathbf{M}\\ {\mathbf{ϵ}}^{(0)\ast }={\mathbf{ϵ}}^{(0)},{\mathbf{\kappa }}^{\ast }=\frac{h}{2}\mathbf{\kappa }\end{array}\}$$

正则化处理后的层合板的内力与应变的关系可以表示为：

$$\left[\begin{array}{c}{\mathbf{N}}^{\ast }\\ {\mathbf{M}}^{\ast }\end{array}\right]=\left[\begin{array}{cc}{\mathbf{A}}^{\ast }& {\mathbf{B}}^{\ast }\\ {\mathbf{B}}^{\ast }& {\mathbf{D}}^{\ast }\end{array}\right]\left[\begin{array}{c}{\mathbf{ϵ}}^{(0)}\\ {\mathbf{\kappa }}^{\ast }\end{array}\right]$$

注意：以上都没有考虑湿热效应的影响。

4 对称层合板的刚度特性

对称层合板是指铺层材料性质对称于板中面的层板。

由于对称层合板相对于中面材料常数${\overline{Q}}_{ij}^{(k)}$、距离$z_k$和厚度$h_k$的对称性，其弹性性质最大的特点是：

$$\mathbf{B}=0$$

其耦合关系如图所示：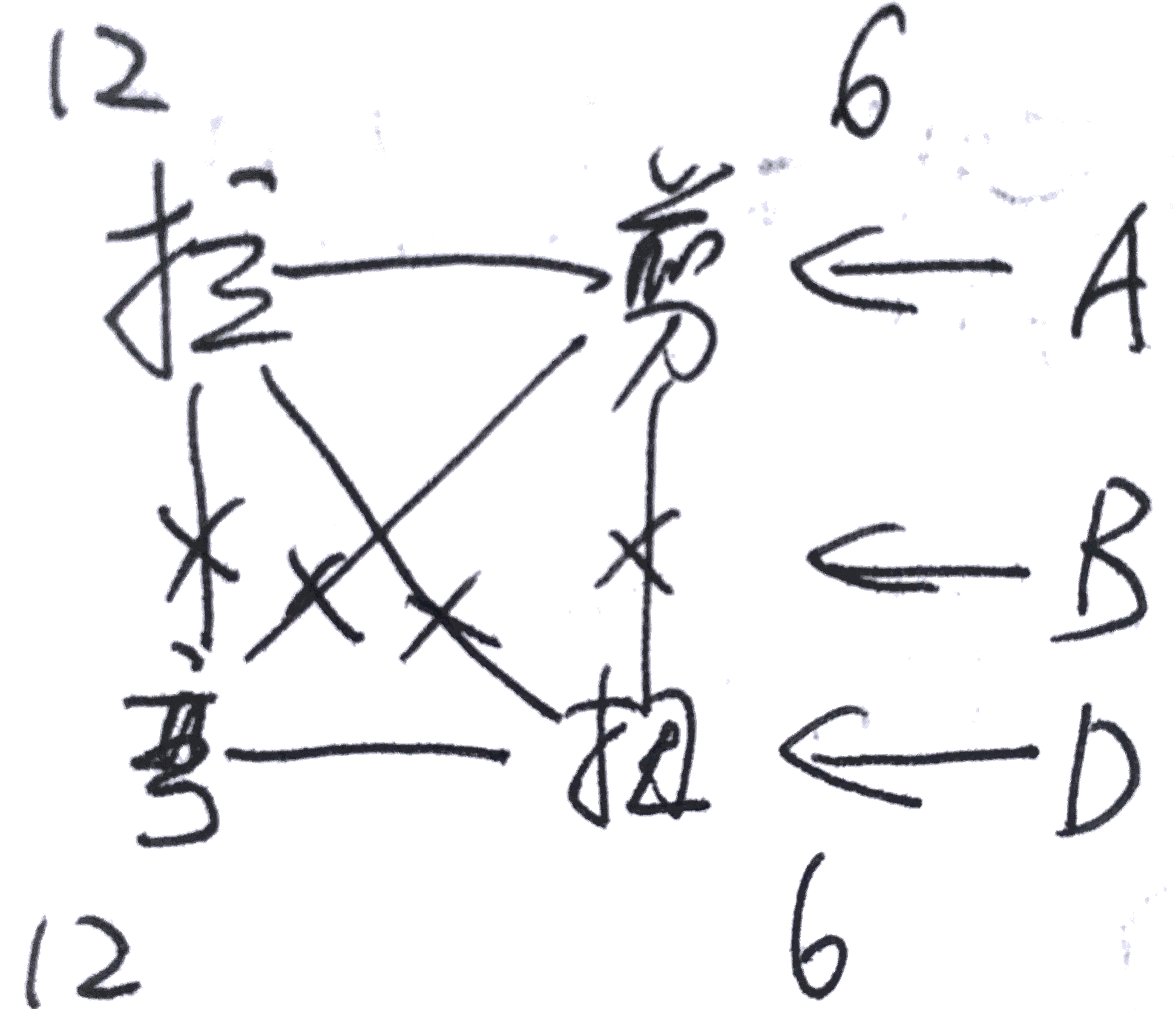

则$(3.3.1)$可简化为：

$$\begin{array}{c}\mathbf{N}=\mathbf{A}{\mathbf{ϵ}}^{(0)}\\ \mathbf{M}=\mathbf{D}\mathbf{\kappa }\end{array}\}\text{\hspace{1em}(4.0.1)}$$

4.1 单层层合板的刚度

单层板可以看成以中面为对称面的对称层合板特例。

1. 当坐标轴方向为材料的正轴方向时，其内力-应变关系为：

   $$\begin{gathered} \left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{21}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\end{array}\right] \\ \left[\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{21}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right]\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right] \end{gathered}$$

   其中：

   $$\begin{gathered} A_{ij}=Q_{ij}t,B_{ij}=0,D_{ij}=\frac{t^3}{12}{Q}_{ij} \\ \begin{array}{c}{Q}_{11}=\frac{E_{\mathrm{L}}}{1-{\nu }_{\mathrm{L}}{\nu }_{\mathrm{T}}},Q_{22}=\frac{E_{\mathrm{T}}}{1-{\nu }_{\mathrm{L}}{\nu }_{\mathrm{T}}},Q_{66}=G_{\mathrm{L}\mathrm{T}}\\ Q_{12}=\frac{{\nu }_{\mathrm{L}}{E}_{\mathrm{L}}}{1-{\nu }_{\mathrm{L}}{\nu }_{\mathrm{T}}}=\frac{{\nu }_{\mathrm{T}}{E}_{\mathrm{T}}}{1-{\nu }_{\mathrm{L}}{\nu }_{\mathrm{T}}},Q_{16}=Q_{26}=0\end{array}\} \end{gathered}$$

   其耦合关系如图所示：
   

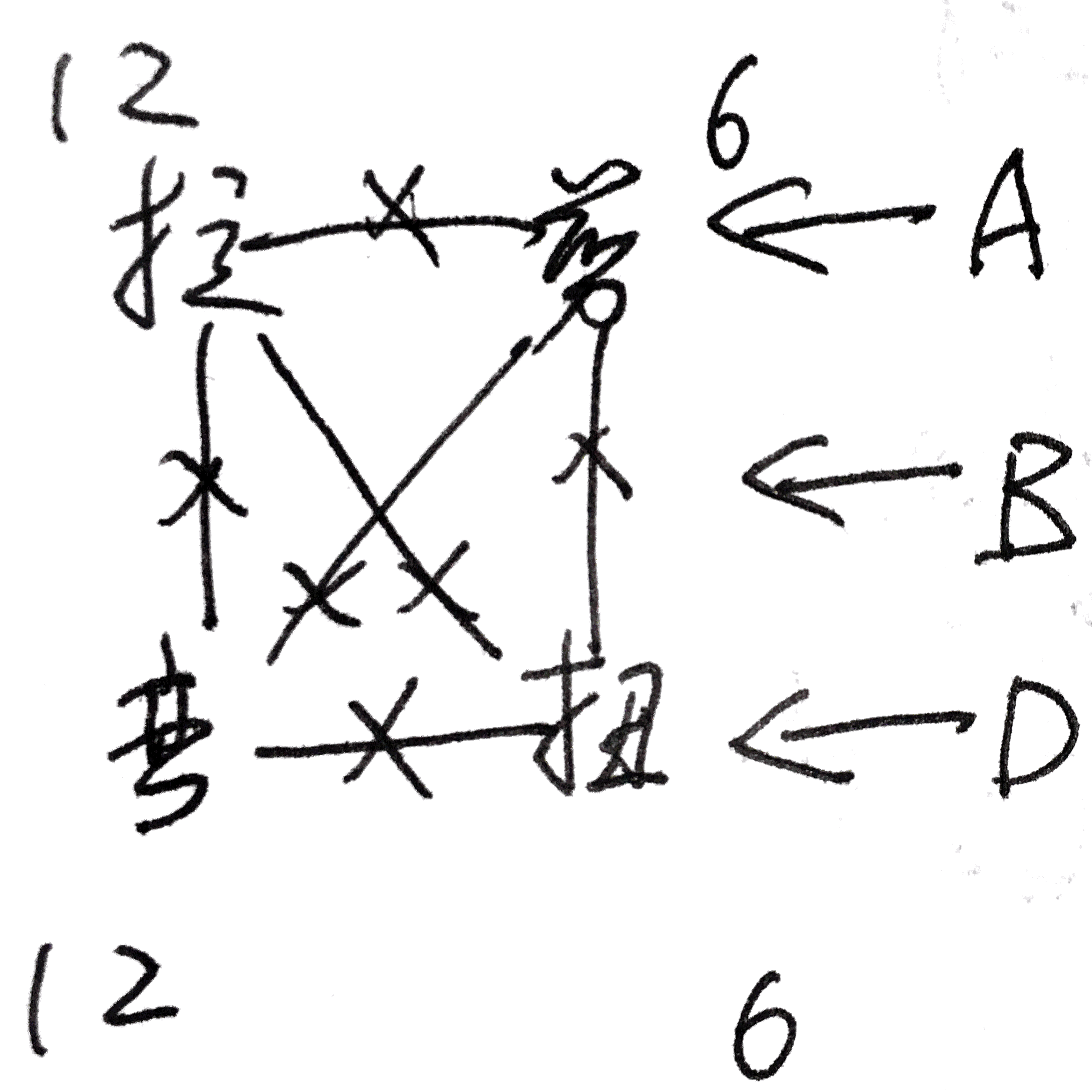
2. 当坐标轴方向为偏轴方向。其内力-应变关系为：

   $$\begin{gathered} \left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{16}\\ A_{21}& A_{22}& A_{26}\\ A_{61}& A_{62}& A_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\end{array}\right] \\ \left[\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{ccc}{D}_{11}& D_{12}& D_{16}\\ D_{21}& D_{22}& D_{26}\\ D_{61}& D_{62}& D_{66}\end{array}\right]\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right] \end{gathered}$$

   其中：

   $$A_{ij}={\overline{Q}}_{ij}t,B_{ij}=0,D_{ij}=\frac{t^3}{12}{\overline{Q}}_{ij}$$

   其耦合关系如图所示：
   

4.2 正交铺设对称层合板的刚度

如果各单层只按0°与90°方向铺设的对称层合板为正交铺设对称层合板。

这类层合板因为$({\overline{Q}}_{16}{)}_k$和$({\overline{Q}}_{26}{)}_k$为零，代入$(3.3.2)$得$A_{16}$、$A_{26}$及$D_{16}$、$D_{26}$为零，其合力-应变关系为：

$$\begin{gathered} \left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{21}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\end{array}\right] \\ \left[\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{21}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right]\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right] \end{gathered}$$

其耦合关系如图所示：

4.3 斜交铺设对称层合板

凡各单层只按±α两种方向铺设的对称层合板为斜交铺设对称层合板。如果两种方向的层数相同，则称为均衡斜交铺设对称层合板。如果两种方向的层数不相同，则称为非均衡的。

由单层材料力学知识：

$$\begin{gathered} {\overline{Q}}_{11}^{(\alpha )}={\overline{Q}}_{11}^{(-\alpha )},{\overline{Q}}_{12}^{(\alpha )}={\overline{Q}}_{12}^{(-\alpha )},{\overline{Q}}_{22}^{(\alpha )}={\overline{Q}}_{22}^{(-\alpha )} \\ {\overline{Q}}_{66}^{(\alpha )}={\overline{Q}}_{66}^{(-\alpha )},{\overline{Q}}_{16}^{(\alpha )}=-{\overline{Q}}_{16}^{(-\alpha )},{\overline{Q}}_{26}^{(\alpha )}=-{\overline{Q}}_{26}^{(-\alpha )} \end{gathered}$$

代入到$(3.3.2)$。对于均衡的斜交对称层合板，若层合板厚度为$h$，则其内力-应变的关系式为：

$$\begin{gathered} \left[\begin{array}{c}{N}_x\\ N_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{12}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\gamma }_{xy}^{(0)}\end{array}\right] \\ \left[\begin{array}{c}{M}_x\\ M_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{12}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right]\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_{xy}\end{array}\right] \end{gathered}$$

其中：

$$\begin{array}{c}{A}_{11}={\overline{Q}}_{11}^{(\alpha )}h,A_{12}={\overline{Q}}_{12}^{(\alpha )}h,A_{22}={\overline{Q}}_{22}^{(\alpha )}h\\ A_{66}={\overline{Q}}_{66}^{(\alpha )}h,A_{16}=A_{26}=0\\ D_{11}=\frac{h^3}{12}{\overline{Q}}_{11}^{(\alpha )},D_{12}=\frac{h^3}{12}{\overline{Q}}_{12}^{(\alpha )},D_{22}=\frac{h^3}{12}{\overline{Q}}_{22}^{(\alpha )}\\ D_{66}=\frac{h^3}{12}{\overline{Q}}_{66}^{(\alpha )}\end{array}\}$$

其耦合关系如图所示：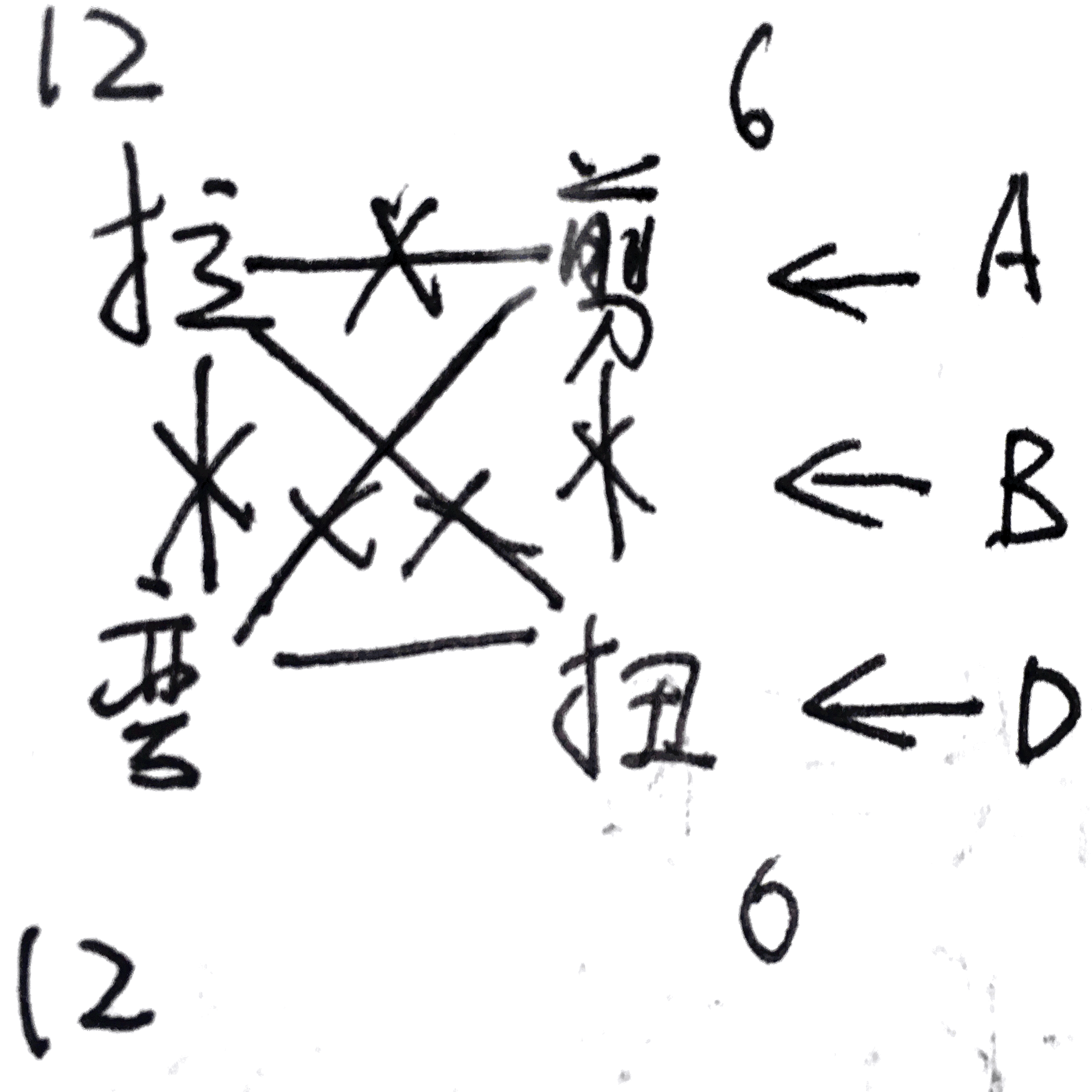

5 两种非对称层合板的刚度

5.1 规则非对称正交铺设层合板

如果层合板仅由0°和90°单层叠合而成，则由于x轴和y轴不管对0°还是90°都是弹性主轴，即$Q_{16}^{(k)}=Q_{26}^{(k)}=0$。因此有

$$\begin{gathered} A_{16}=A_{26}=0 \\ {B}_{16}=B_{26}=0 \\ {D}_{16}=D_{26}=0 \end{gathered}$$

则其耦合关系如图所示：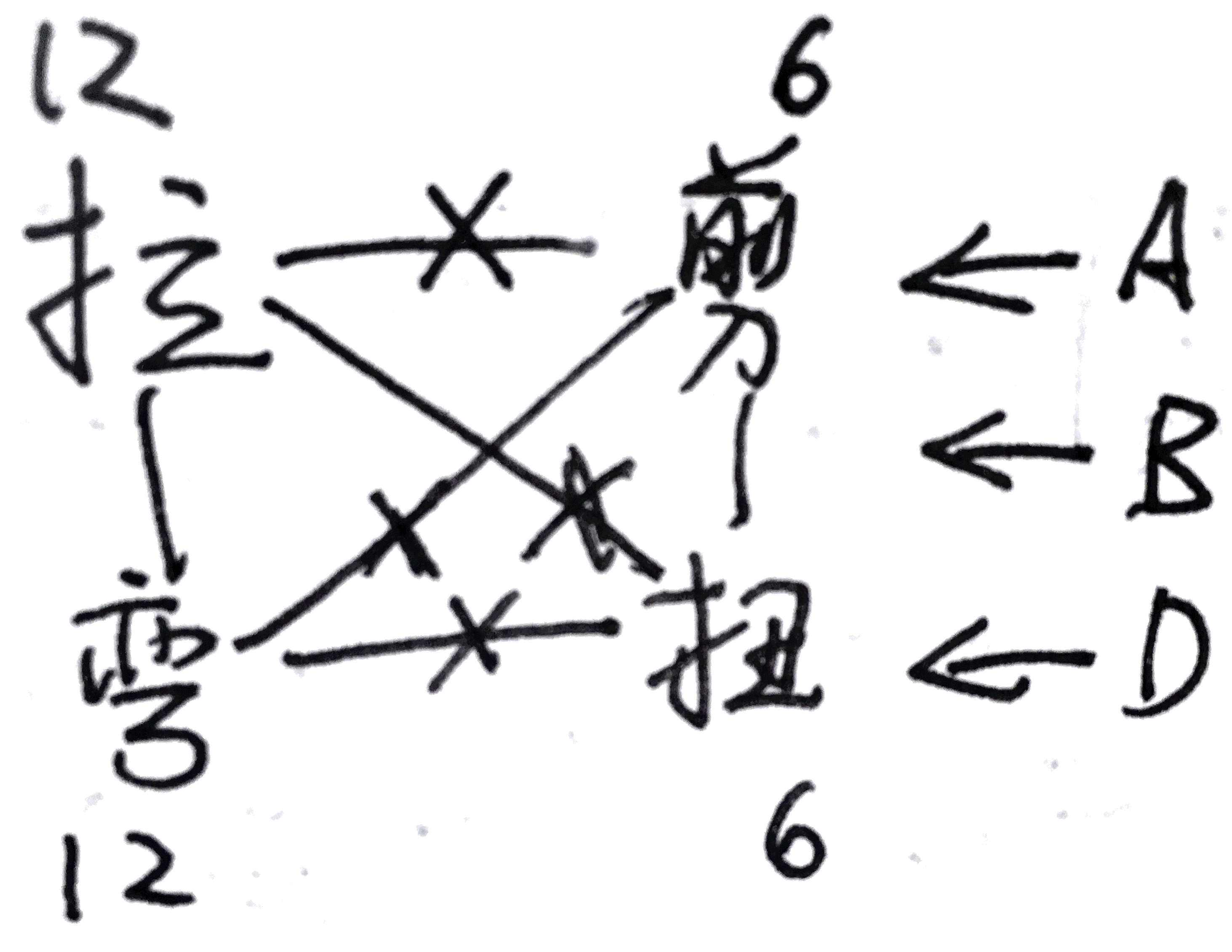

特殊地，若0°和90°层交替排列，每一铺层组有相同层数，单层厚度相等，材料性能一样，这类层合板被称为规则非对称正交铺设层合板。除了上式以外，还满足：

$$\begin{gathered} B_{12}=B_{66}=0 \\ {A}_{11}=A_{22},D_{11}=D_{22},B_{11}=-B_{22} \end{gathered}$$

则，其耦合关系如图所示：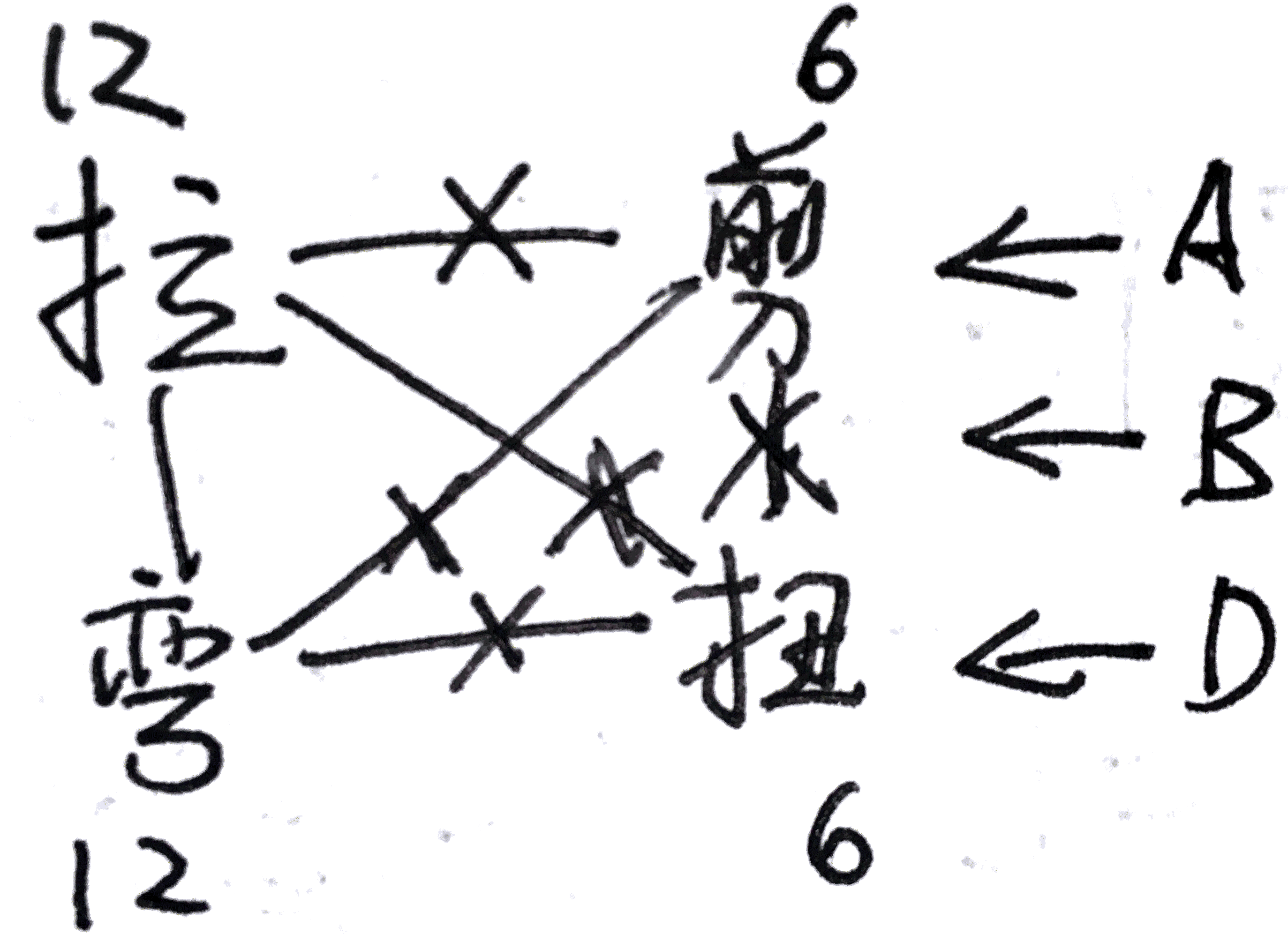

且，x和y方向的拉与对方方向的弯不耦合。x和y方向的拉对自身方向的拉伸刚度相等。x和y方向的弯对自身方向的弯曲刚度相等。x和y方向的拉与自身方向的弯的耦合效果相反。

可以看出，当它主要承受剪切，扭转载荷时，就像均质板一样变形。

5.2 规则反对称层合板

如果相对于板中面对称位置$(z=\pm z_i)$上的两个单层由同样材料做成，厚度相等，且满足$\theta (z_i)=-\theta (-z_i)$的条件，这样的板就被称为反对称板。一般反对称板均由偶数的单层组成，但当中间层的铺层角为0°或90°时，也可以由奇数层组成。

由反对称的特性，不难求得

$$A_{16}=A_{26}=D_{16}=D_{26}=0$$

其耦合关系如图所示：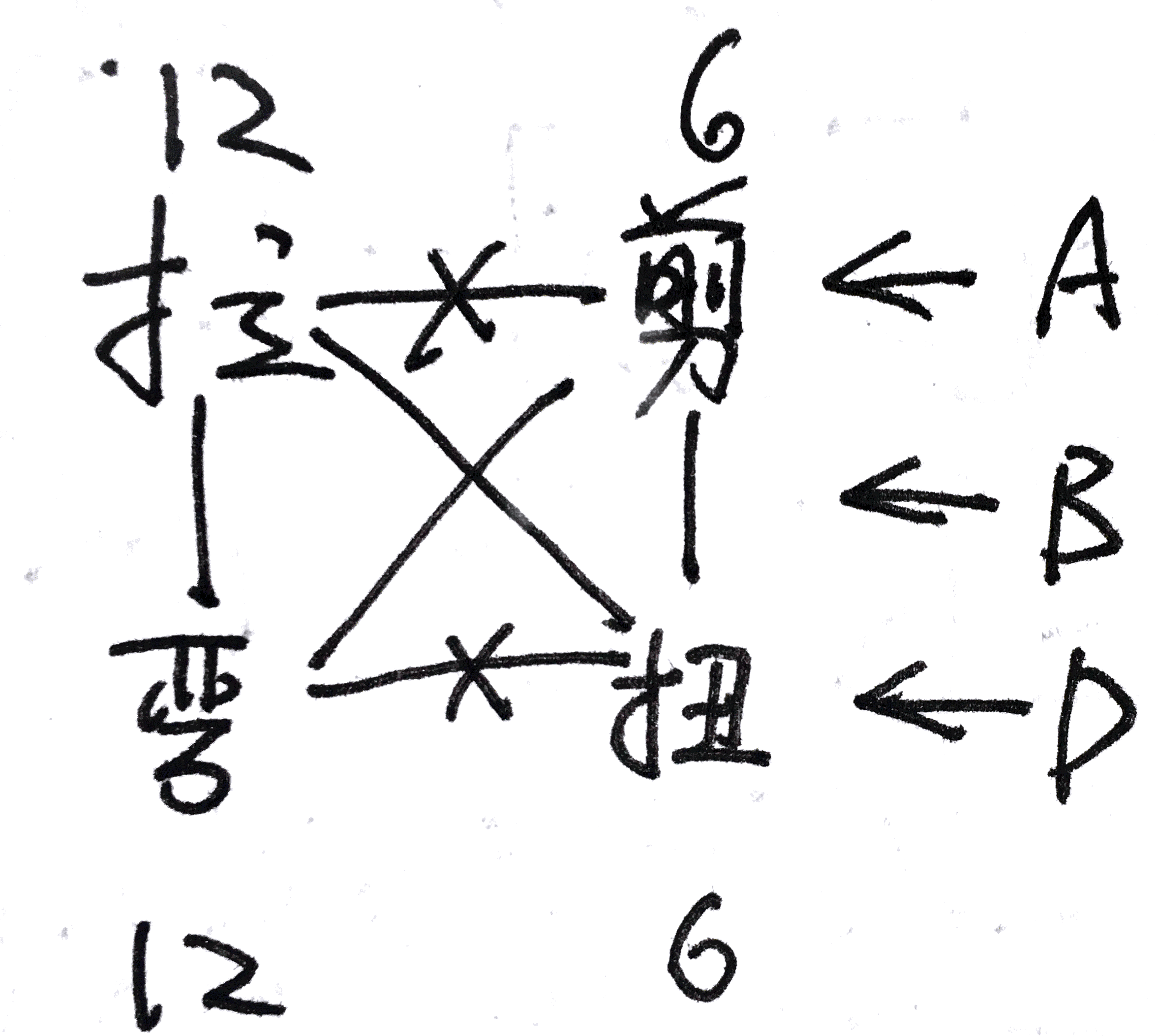

特殊地，当组成反对称板的各单层或各铺层组厚度相等，材料性能相同，其铺层角为$+\theta$或$-\theta$，则称这种板为规则反对称层合板。其应在上式的基础上满足：

$$B_{11}=B_{22}=B_{12}=B_{66}=0$$

则耦合关系如图所示：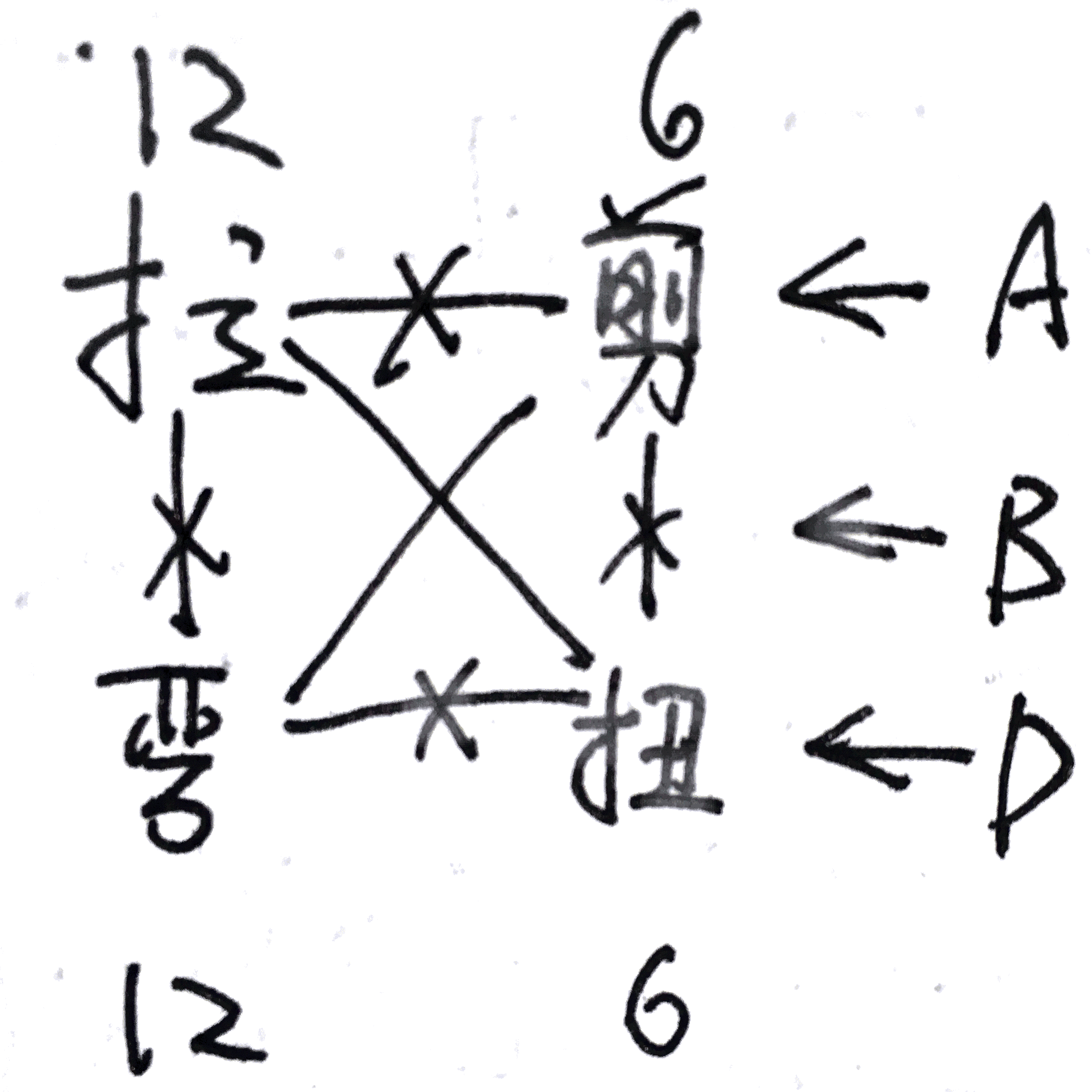

则可以将它的内力-应变关系$(3.3.3)$改写作：

$$\left[\begin{array}{c}{N}_x\\ N_y\\ M_{xy}\\ M_x\\ M_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{cccccc}{A}_{11}& A_{12}& B_{16}& 0& 0& 0\\ A_{21}& A_{22}& B_{26}& 0& 0& 0\\ B_{61}& B_{62}& D_{66}& 0& 0& 0\\ 0& 0& 0& D_{11}& D_{12}& B_{16}\\ 0& 0& 0& D_{21}& D_{22}& B_{26}\\ 0& 0& 0& B_{61}& B_{62}& A_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\kappa }_{xy}\\ {\kappa }_x\\ {\kappa }_y\\ {\gamma }_{xy}^{(0)}\end{array}\right]$$

或写成：

$$\begin{gathered} \left[\begin{array}{c}{N}_x\\ N_y\\ M_{xy}\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& B_{16}\\ A_{21}& A_{22}& B_{26}\\ B_{61}& B_{62}& D_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x^{(0)}\\ {ϵ}_y^{(0)}\\ {\kappa }_{xy}\end{array}\right] \\ \left[\begin{array}{c}{M}_x\\ M_y\\ N_{xy}\end{array}\right]=\left[\begin{array}{ccc}{D}_{11}& D_{12}& B_{16}\\ D_{21}& D_{22}& B_{26}\\ B_{61}& B_{62}& A_{66}\end{array}\right]\left[\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\gamma }_{xy}^{(0)}\end{array}\right] \end{gathered}$$

6 平行移轴定理

前面讨论的层合板刚度系数，都是将参考坐标系z的坐标原点（也即$Oxy$坐标面）置于层合板的几何中面上，因此所求得刚度系数被称为层合板中面刚度系数。下面讨论非中面刚度系数。

如图所示，设层合板中面处为坐标$z=0$，与中面平行且距离为$d$的面为$z^{\prime }=0$，则层合板中任意点的坐标为$z^{\pr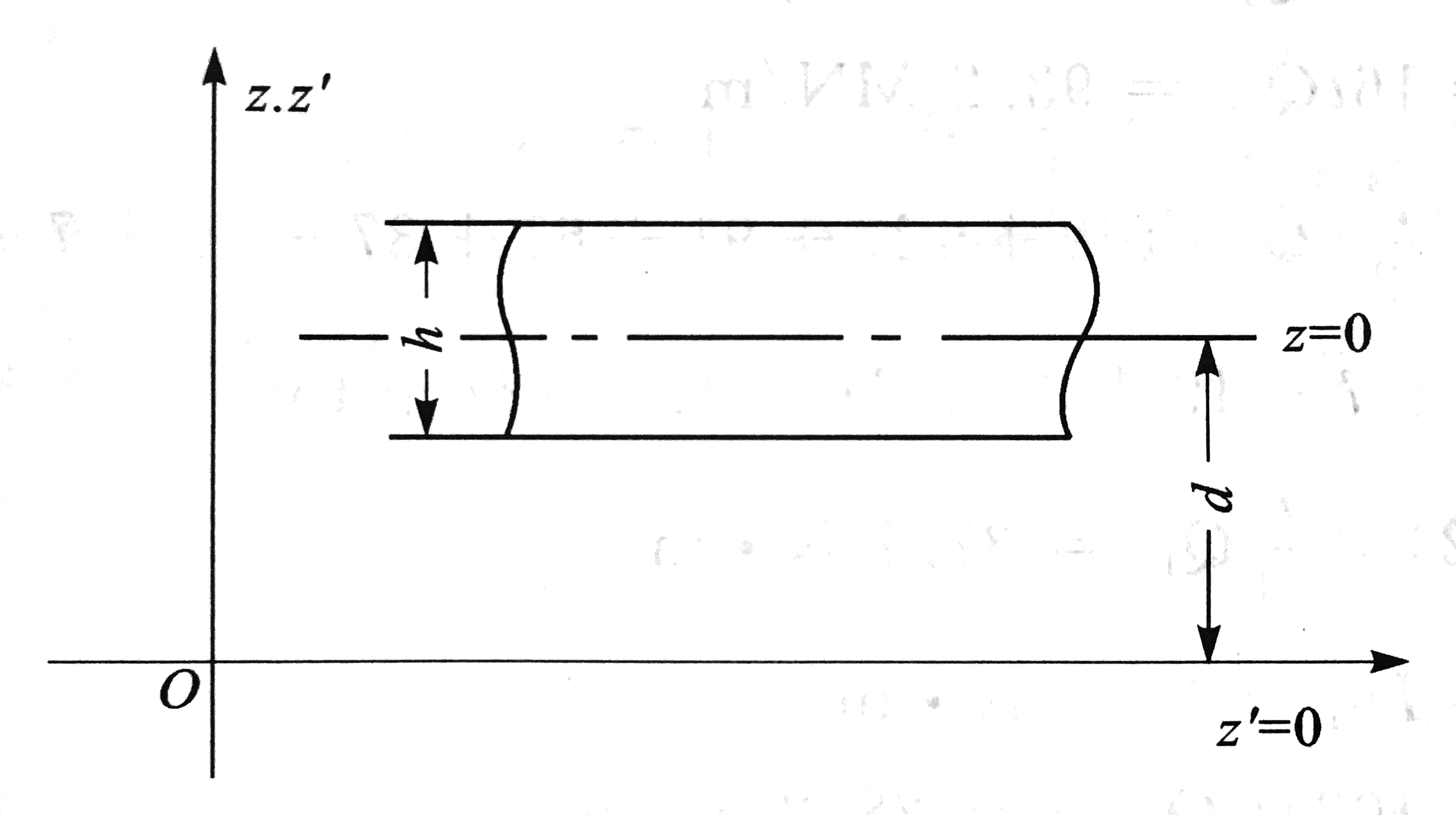ime }=z+d$。

根据上述坐标关系，两个面的刚度系数之间的关系为：

$$\begin{gathered} A_{ij}^{\prime }={\int }_{d-\frac{h}{2}}^{d+\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}\mathrm{d}{z}^{\prime }={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}\mathrm{d}z=A_{ij} \\ {B}_{ij}^{\prime }={\int }_{d-\frac{h}{2}}^{d+\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}{z}^{\prime }\mathrm{d}{z}^{\prime }={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}(z+d)\mathrm{d}z=B_{ij}+d{A}_{ij} \\ {D}_{ij}^{\prime }={\int }_{d-\frac{h}{2}}^{d+\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}{z}^{\prime 2}\mathrm{d}{z}^{\prime }={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}(z+d{)}^2\mathrm{d}z \\ ={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\overline{Q}}_{ij}^{(k)}(z^2+2dz+d^2)\mathrm{d}z=D_{ij}+2d{B}_{ij}+d^2{A}_{ij} \end{gathered}$$

根据作用在板单位宽度上的内力和内力矩的定义，对$O{x}^{\prime }{y}^{\prime }{z}^{\prime }$坐标系，有：

$$\begin{gathered} N_i^{\prime }={\int }_{d-\frac{h}{2}}^{d+\frac{h}{2}}{\sigma }_i\mathrm{d}{z}^{\prime }={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\sigma }_i\mathrm{d}z=N_i \\ {M}_i^{\prime }={\int }_{d-\frac{h}{2}}^{d+\frac{h}{2}}{\sigma }_i{z}^{\prime }\mathrm{d}{z}^{\prime }={\int }_{-\frac{h}{2}}^{\frac{h}{2}}{\sigma }_i(z+d)\mathrm{d}z=M_i+d{N}_i \end{gathered}$$

以上关系为层合板的平行移轴定理。

对刚度系数进行正轴化处理，可得：

$$\begin{array}{c}{A_{ij}^{\ast }}^{\prime }=A_{ij}^{\ast }\\ {B_{ij}^{\ast }}^{\prime }=B_{ij}^{\ast }+2A_{ij}^{\ast }d/h\\ {D_{ij}^{\ast }}^{\prime }=D_{ij}^{\ast }+12B_{ij}^{\ast }d/h+12A_{ij}^{\ast }(d/h{)}^2\end{array}\}$$

7 湿热效应对层合板刚度影响

树脂基体是吸湿的，随着吸湿扩散，结构会出现不同的吸湿量分布。这会降低纤维的抗腐蚀阻力，降低其刚度和强度。

7.1 单层的湿热变形

正轴向的湿热自由应变关系式为：

$$\left[\begin{array}{c}{e}_1\\ e_2\\ e_{12}\end{array}\right]=\left[\begin{array}{cc}{\alpha }_{\mathrm{L}}& {\beta }_{\mathrm{L}}\\ {\alpha }_{\mathrm{T}}& {\beta }_{\mathrm{T}}\\ 0& 0\end{array}\right]\left[\begin{array}{c}\Delta T\\ C\end{array}\right]$$

其中， ${\alpha }_{\mathrm{L}}$、${\alpha }_{\mathrm{T}}$分别为纵向、横向热膨胀系数；${\beta }_{\mathrm{L}}$、${\beta }_{\mathrm{T}}$分别为纵向、横向湿膨胀系数；$\Delta T$为温度变化量，$C$为水分含量，由下式定义：

$$C=\underset{\Delta \to 0}{\lim }\frac{\Delta V中的水分含量}{\Delta V中干燥的复合材料的质量}$$

偏轴情况下，关系式变为：

$$\left[\begin{array}{c}{e}_x\\ e_y\\ e_{xy}\end{array}\right]=\left[\begin{array}{cc}{\alpha }_x& {\beta }_x\\ {\alpha }_y& {\beta }_y\\ {\alpha }_{xy}& {\beta }_{xy}\end{array}\right]\left[\begin{array}{c}\Delta T\\ C\end{array}\right]$$

其中，${\alpha }_a$、${\alpha }_y$、${\alpha }_{xy}$和${\beta }_x$、${\beta }_y$、${\beta }_{xy}$可以通过单层材料力学中的应力转换公式由${\alpha }_{\mathrm{L}}$、${\alpha }_{\mathrm{T}}$和${\beta }_a$、${\beta }_{\mathrm{T}}$求得。

7.2 含湿热应变的单层应力应变关系

单层在既有机械应力，又有温度和水分含量变化引起的小变形的情况下，利用叠加原理可得正轴时包含湿热应变的应变-应力关系式：

$$\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ {\gamma }_{12}\end{array}\right]=\left[\begin{array}{ccc}{S}_{11}& S_{12}& 0\\ S_{21}& S_{22}& 0\\ 0& 0& S_{66}\end{array}\right]\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\tau }_{12}\end{array}\right]+\left[\begin{array}{c}{e}_1\\ e_2\\ 0\end{array}\right]$$

偏轴时包含湿热应变的应变-应力关系式为：

$$\left[\begin{array}{c}{ϵ}_x\\ {ϵ}_y\\ {\gamma }_{xy}\end{array}\right]=\left[\begin{array}{ccc}{\overline{S}}_{11}& {\overline{S}}_{12}& {\overline{S}}_{16}\\ {\overline{S}}_{21}& {\overline{S}}_{22}& {\overline{S}}_{26}\\ {\overline{S}}_{61}& {\overline{S}}_{62}& {\overline{S}}_{66}\end{array}\right]\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right]+\left[\begin{array}{c}{e}_x\\ e_y\\ e_{xy}\end{array}\right]\text{\hspace{1em}(7.2.1)}$$

7.3 含湿热效应的层合板内力-应变关系

第3节没有考虑湿热效应，于是可利用$(7.2.1)$修正$(3.2.3)$为：

$${\mathbf{\sigma }}^{(k)}={\overline{\mathbf{Q}}}^{(k)}({\mathbf{ϵ}}^{(0)}+z\mathbf{\kappa }-\mathbf{e})$$

假设温度、湿度不沿$z$方向变化。于是与3.3节同理可推得：

$$\begin{array}{c}\mathbf{N}=\mathbf{A}({\mathbf{ϵ}}^{(0)}-\mathbf{e})+\mathbf{B}\mathbf{\kappa }\\ \mathbf{M}=\mathbf{B}({\mathbf{ϵ}}^{(0)}-\mathbf{e})+\mathbf{D}\mathbf{\kappa }\end{array}\}$$

令

$$\begin{gathered} {\mathbf{N}}^{\mathbf{T}}=\mathbf{A}\mathbf{e} \\ {\mathbf{M}}^{\mathbf{T}}=\mathbf{B}\mathbf{e} \end{gathered}$$

即：使层合板产生相同湿热自由应变的湿热等效内力。（注意：这个内力是不存在的，不计入内力中）于是：

$$\begin{array}{c}\mathbf{N}+{\mathbf{N}}^{\mathbf{T}}=\mathbf{A}{\mathbf{ϵ}}^{(0)}+\mathbf{B}\mathbf{\kappa }\\ \mathbf{M}+{\mathbf{M}}^{\mathbf{T}}=\mathbf{B}{\mathbf{ϵ}}^{(0)}+\mathbf{D}\mathbf{\kappa }\end{array}\}\text{\hspace{1em}(7.3.1)}$$

若令$\overline{\mathbf{N}}=\mathbf{N}+{\mathbf{N}}^{\mathbf{T}},\overline{\mathbf{M}}=\mathbf{M}+{\mathbf{M}}^{\mathbf{T}}$，为层合板的等效总内力，则：

$$\begin{array}{c}\overline{\mathbf{N}}=\mathbf{A}{\mathbf{ϵ}}^{(0)}+\mathbf{B}\mathbf{\kappa }\\ \overline{\mathbf{M}}=\mathbf{B}{\mathbf{ϵ}}^{(0)}+\mathbf{D}\mathbf{\kappa }\end{array}\}$$

得到了与$(3.3.1)$相似的关系式。

8 层合板的强度

影响层合板的强度的因素有：各层的强度、各层的刚度、各层的热膨胀系数、各层的方向、各层的厚度、叠合顺序及固化温度等。

表征层合板的强度指标主要有：

1. 最先一层失效强度：外力作用下，层合板最先一层失效时的层合板正则化内力；

2. 极限强度：层合板单层全部失效时层合板正则化内力；

3. 层合板的宏观各向异性强度：通过实验测定的层合板在单向载荷下的基本力学性能。

8.1 最先一层失效强度

计算时，必须先做层合板的单层应力分析，然后利用强度比方程计算层合板的各个单层的强度比，强度比最小的单层先失效。其对应的层合板的正则化内力即为所求强度，如图所示：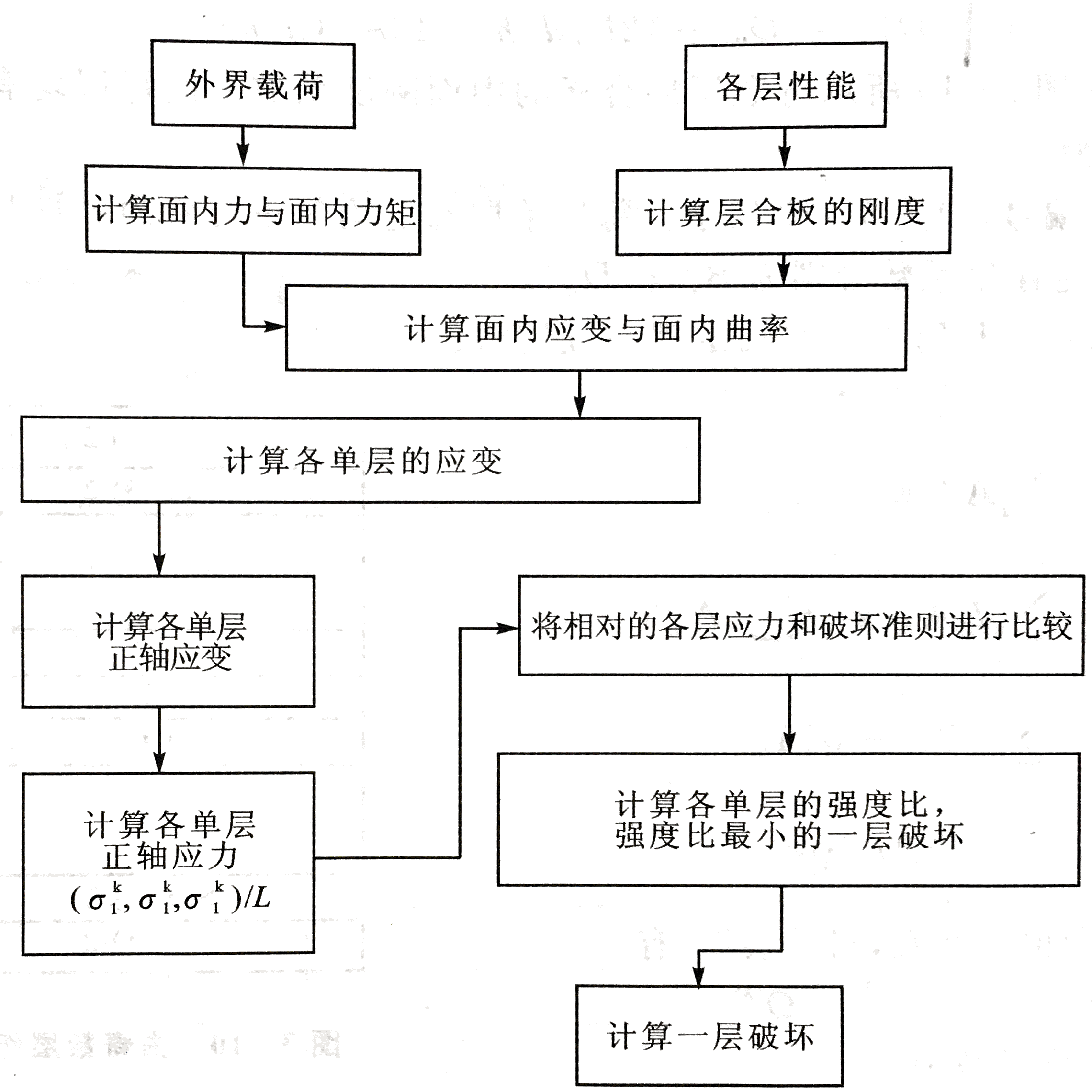

8.2 极限强度

极限强度的计算是在最先一层失效强度计算步骤的基础上，套上循环。如图所示：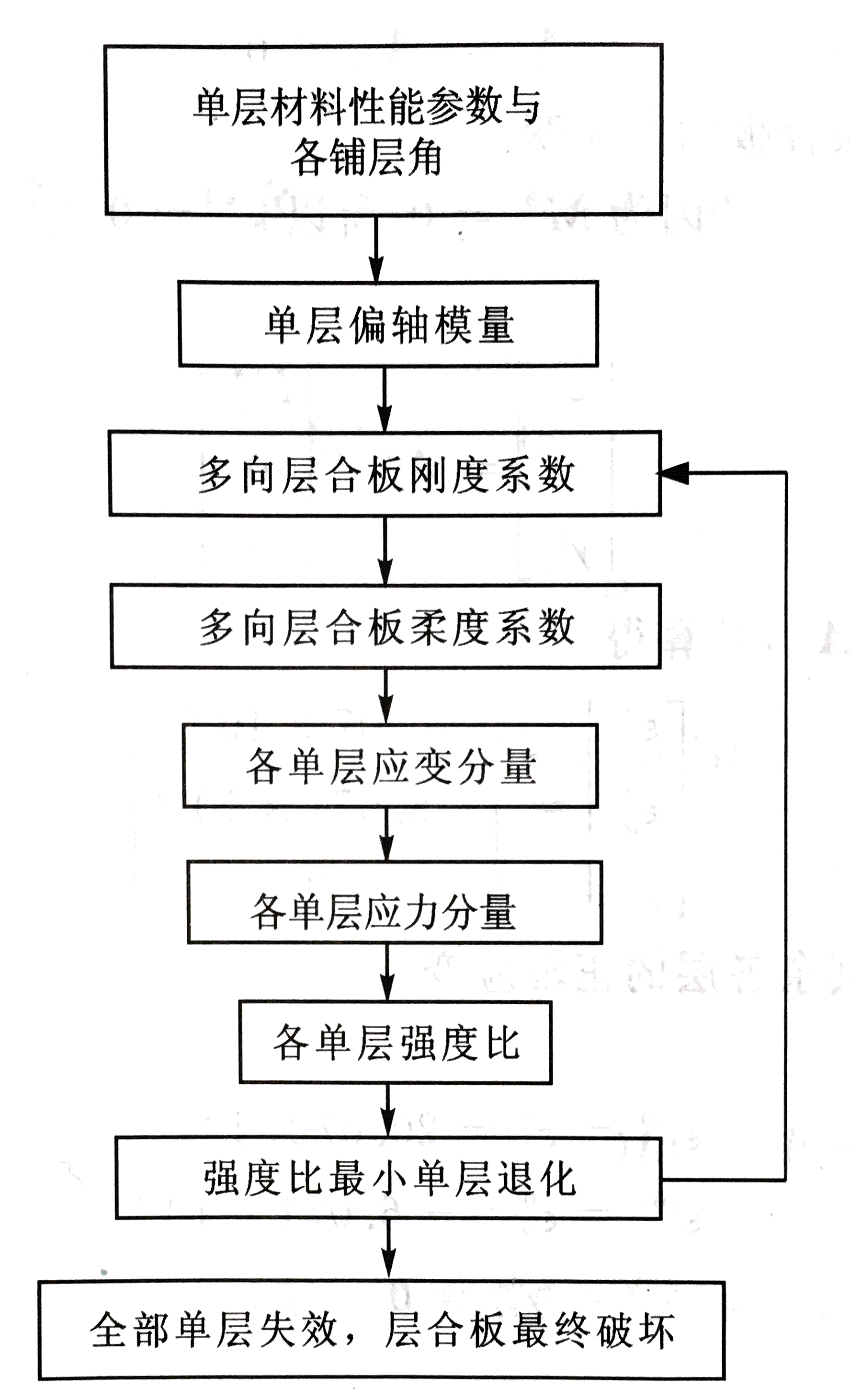

一般对于失效层退化可按照如下假定处理：
若${\sigma }_1<X$，则$Q_{11}=Q_{12}=Q_{66}=0$；
若${\sigma }_1\ge X$，则$Q_{11}=Q_{22}=Q_{12}=Q_{66}=0$。
且失效退化后整个层合板仍按经典层合理论计算刚度。

8.3 湿热效应对层合板强度的影响

8.3.1 层合板的残余应变和残余应力

需要明确的是：湿热本身只会产生应变，不产生应力。只有在有位移边界条件时可以间接产生应力。

则可以定义：应力=机械应力+位移边界条件应力，应变=机械应变+湿热自由应变+位移边界条件应变。即：

$$\begin{gathered} \mathbf{\sigma }={\mathbf{\sigma }}^{\mathbf{M}}+{\mathbf{\sigma }}^{\mathbf{R}} \\ \mathbf{ϵ}={\mathbf{ϵ}}^{\mathbf{M}}+{\mathbf{ϵ}}^{\mathbf{R}}+\mathbf{e} \end{gathered}$$

其中，${\mathbf{\sigma }}^{\mathbf{M}}$为机械应力，等于只有机械载荷作用下的应力。${\mathbf{\sigma }}^{\mathbf{R}}$为位移边界条件应力，等于有位移边界条件时的总应力和无位移边界条件时的总应应力的差值（或只有支反力作用下产生的应力）。${\mathbf{ϵ}}^{\mathbf{M}}$为机械应变，等于只有机械载荷作用下的应变。$\mathbf{e}$为湿热自由应变，等于只有湿热效应影响下的应变。${\mathbf{ϵ}}^{\mathbf{R}}$为位移边界条件应变，等于有位移边界条件时的总应变和无位移边界条件时的总应变的差值（或只有支反力作用下产生的应变）。

${\mathbf{ϵ}}^{\mathbf{R}}$和${\mathbf{\sigma }}^{\mathbf{R}}$也分别叫残余应变和残余应力。

如图所示，在湿热变形下，由于不同单层的自由应变不同，而单层和单层之间没有相对位移，它们相互形成位移边界条件。于是湿热变形引起了残余应变和残余应力：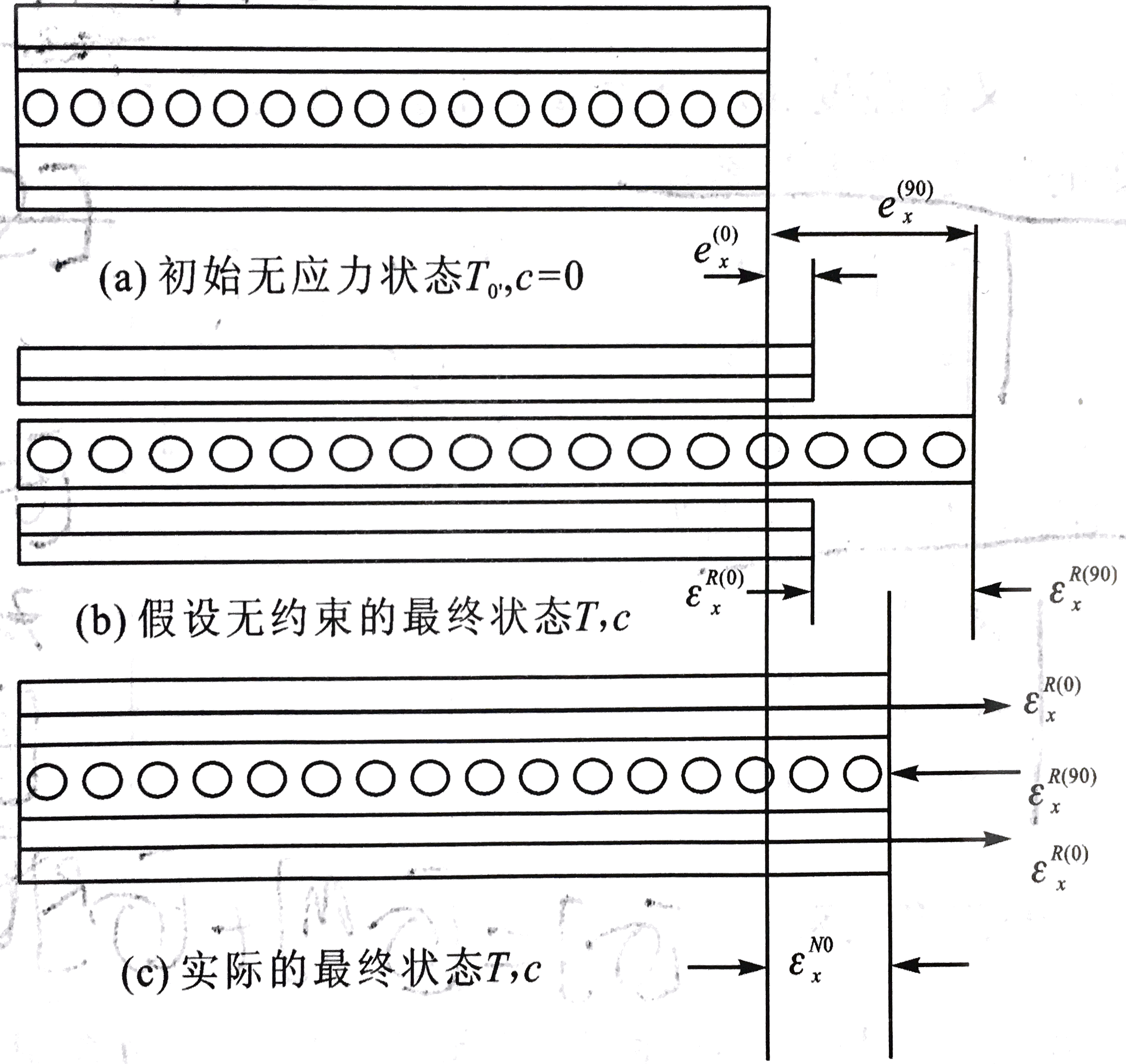

在无机械载荷的状态下：

$$\mathbf{ϵ}={\mathbf{ϵ}}^{\mathbf{N}}=\mathbf{e}+{\mathbf{ϵ}}^{\mathbf{R}}$$

所以层合板的残余应变为：

$${\mathbf{ϵ}}^{\mathbf{R}}={\mathbf{ϵ}}^{\mathbf{N}}-\mathbf{e}$$

与层合板残余应变对应的层合板残余应力为：

$${\mathbf{\sigma }}^{\mathbf{R}}=\overline{\mathbf{Q}}{\mathbf{ϵ}}^{\mathbf{R}}$$

8.3.2 考虑残余应力的层合板强度计算

应用强度比方程时，要求各个待考察的应力分量是呈比例增加的。在有残余应力的情况下，残余应力是不随机械载荷的增大而增大的。故残余应力不能计入要考察的应力分量中。于是，强度比以外载荷作用下的应力${\sigma }_i^M$为基准：

$$R=\frac{{\sigma }_{i(a)}^M}{{\sigma }_i^M}$$

故考虑残余应力的强度比方程，只要在以往的强度比方程中将$R$去掉，而把${\sigma }_i$改为$R{\sigma }_i^M+{\sigma }_i^R$即可。

例如，蔡-胡失效准则的强度比方程，在考虑残余应力时可改为：

$$\begin{gathered} F_{11}(R{\sigma }_1^M+{\sigma }_1^R{)}^2+2F_{12}(R{\sigma }_1^M+{\sigma }_1^R)(R{\sigma }_2^M+{\sigma }_2^R)+ \\ {F}_{22}(R{\sigma }_2^M+{\sigma }_2^R{)}^2+F_{66}(R{\sigma }_6^M+{\sigma }_6^R{)}^2+ \\ {F}_1(R{\sigma }_1^M+{\sigma }_1^R)+F_2(R{\sigma }_2^M+{\sigma }_2^R)-1=0 \end{gathered}$$

具体计算流程如图所示：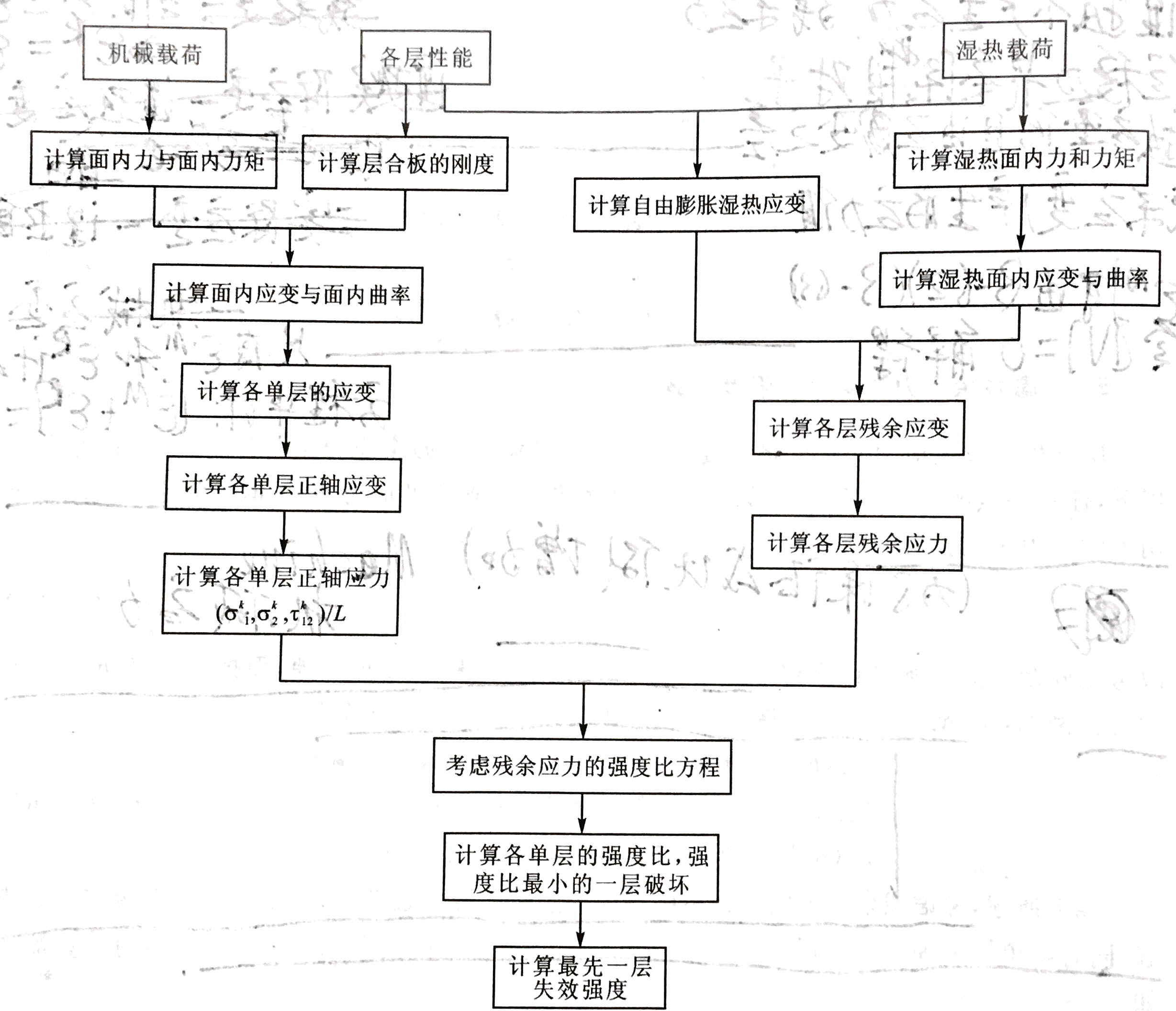

9 总结

1. 层合板的应力随厚度方向为非线性分布。所以不研究应力-应变关系，转而研究内力-应变关系。

2. 层合板往往会有拉-剪-弯-扭耦合。对于对称层合板，无拉剪-弯扭耦合，但可能有拉-剪耦合、弯-扭耦合。对于规则非对称正交铺设层合板，无拉-剪、弯-扭、拉-扭、弯-剪、剪-扭耦合，且其拉-弯耦合也具有特殊性。对于规则反对称层合板，无拉-剪、弯-扭、拉-弯、剪-扭耦合。

3. 湿热效应会产生湿热自由应变。然而若没有位移边界条件，则不会产生应力。在有位移边界条件的情况下，也只能算作位移边界条件引起的应力。即湿热效应只能通过位移边界条件间接产生应力。

4. 获得层合板的强度有预测方法和实验方法。预测方法的强度指标为最先一层失效强度和或极限强度。是将层合板的每个单层的应力和应变算出后，分别用复合材料的强度理论并代入强度比，进行分析判断。当考虑湿热效应时，强度比则定义为机械应力极限/机械应力，即排除残余应力。

---

本文章使用limfx的vsocde插件快速发布